Aprendiendo diseño naval

En algunos de mis textos de este blog creo haber dicho que soy muy aficionado al diseño naval. Hubiera disfrutado enormemente diseñando y construyendo por mi mismo un barco para navegar en él, algo que no he podido ni creo que pueda, motivo por el que me he “enganchado” a una afición “a escala”, que me permite matar parte del gusanillo: el modelismo naval. A causa de ello, he visitado innumerables páginas dedicadas a esta afición, en las que he visto realizaciones de magníficos modelistas que, más de una vez, me han dejado boquiabierto, pero no recuerdo haber visto en ninguna de esas páginas el método seguido para diseñar la forma del casco, pues, sin excepción, comienzan la construcción del modelo por sus cuadernas, partiendo de un diseño creado, aparentemente, por generación espontánea, y al que no parece que ninguno le conceda importancia, algo con lo que estoy frontalmente en desacuerdo.
En consecuencia, retomo de nuevo el diseño naval como tema (ver http://ganandobarlovento.es/diseno-naval-iniciacion/ ), para explicar el método que sigo para trazar el plano de formas de los modelos de embarcaciones radio controladas (RC), que posteriormente construyo. Soy consciente de que las técnicas que explicaré son, desde hace tiempo, aplicadas con enorme rapidez, precisión y exactitud por magníficos programas de diseño 3D (en tres dimensiones), sin que, quienes los usan, se preocupen de hacer ciertas operaciones y comprobaciones de trazado, a las que, en las explicaciones que siguen, me referiré y de las que haré bastante hincapié. Aclaro que, lo siguiente, es la descripción de uso de aquellos conceptos geométricos en que se basa el trazado del plano de formas de cualquier barco, real o a escala, plano éste básico y fundamental en el que irremisiblemente deberá basarse cualquier otro que se haga de ellos.
Añado que, para la explicación de los trazados, solo haré referencia a métodos informáticos de diseño 2D (en dos dimensiones).
Dicho lo cual, comenzaré diciendo una obviedad, pues es evidente que el primer paso para la construcción de un modelo consiste en elegir tipo y tamaño que, en cualquier caso, responderá a una de las características siguientes:
a – réplica a escala reducida de un barco real, existente o que haya existido.
b – réplica a escala reducida de un determinado tipo de barco, sin que responda a ninguno real.
c – de tipo y dimensiones ajustadas a una determinada normativa.
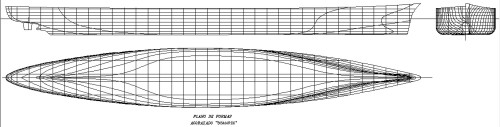
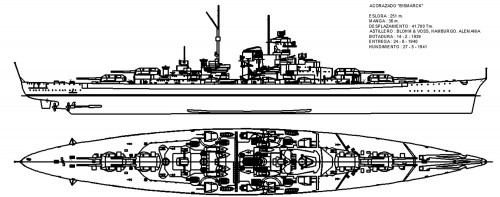
Cualquier modalidad elegida requerirá la recopilación de todos cuantos datos puedan conseguirse para poderlo confeccionar y, concretamente en el caso “a”, es imprescindible conocer las dimensiones principales del barco en cuestión, disponer de sus planos de disposición general y el de formas y, adicionalmente, es enormemente beneficioso disponer de todas cuantas fotografías ilustren sus detalles y aspecto. Para quien no esté familiarizado con la terminología naval, muestro como ejemplos en las Fig. 1 y 2 el planos de formas y el de disposición general, respectivamente, de un famoso e histórico barco de guerra; a partir de ellos, podría hacerse una aceptable réplica a escala del barco real.

Fig. 1

Fig. 2

En el caso “b” es el de mayor libertad para el modelista pues, el modelo que diseñe y construya con este criterio, solo debe respetar el aspecto general del tipo de barco real que haya elegido, por lo que también debe recopilar toda cuanta información sobre ellos pueda conseguir.
El caso “c” hace referencia a aquellos modelos cuyo diseño y construcción deben cumplir los requisitos de determinadas reglamentaciones, una cuestión fundamental para que puedan competir en ciertas regatas de modelos RC, sometidas a la supervisión de organizaciones tal como la International Radio Sailing Association; seguramente existen otras organizaciones relacionadas con el modelismo naval radio controlado, pero, hoy por hoy, solo conozco la citada. Entre otras modalidades, la asociación tutela el modelismo RC de la clase IOM (International One Metre), que básicamente son modelos de vela radio controlados con eslora de 1 m., que tienen para mí gran atractivo, motivo por el que serán ellos los que me sirvan para explicar mi manera de trazar su plano de formas (plano de líneas, como dicen otros).
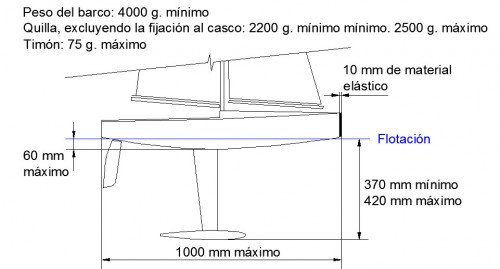
Para los IOM – como los llamaré a partir de ahora – la antedicha asociación tiene publicados varios documentos entre los que se encuentra el conocido con el nombre de «International One Metre. Class Rules 2013», en el que se especifican, entre otros temas, ciertos requisitos de diseño y construcción (para quien quiera leerlo, existen en Internet sus .pdf en versiones inglés y español). En la Fig. 3 he marcado las restricciones que impone este documento a determinadas dimensiones y características del casco de los IOM.

Fig. 3

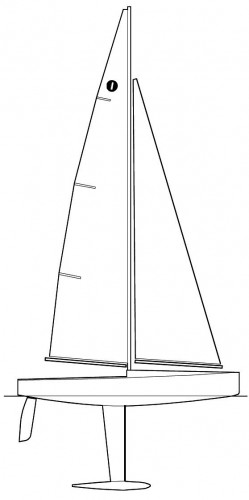
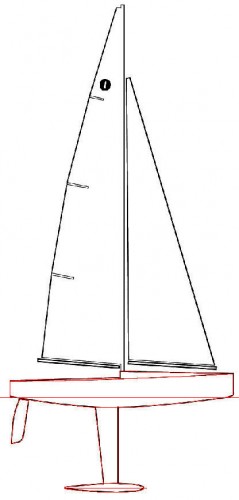
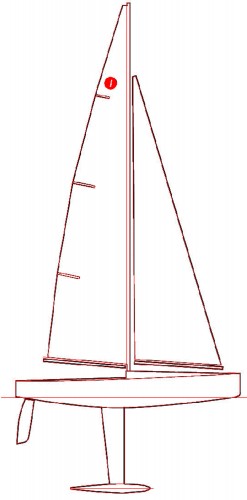
Dicho lo anterior, paso ahora a explicar el proceso, propiamente dicho, de la confección del plano de formas de un IOM. Con tal finalidad, localicé en Internet su alzado y, concretamente, el que se ve en la Fig. 4 está tomado de la portada del documento en .pdf «International One Metre. Class Rules 2013», del que realicé una captura de pantalla que posteriormente recorté utilizando para ello un programa de tratamiento de imágenes, a lo que siguió un grabado de la misma en formato .jpg; seguidamente copié esta imagen y la pegue en el área de trazado del programa de CAD que utilizo, hecho lo cual, tracé sobre sus líneas negras otras líneas rojas (con objeto de distinguir unas de otras) valiéndome de los medios de trazado del propio programa; el resultado parcial de esta operación es visible en la Fig. 5, y el total en la Fig. 6.

Fig. 4

Fig. 5

Fig. 6

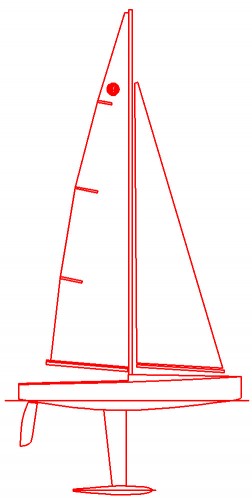
Hecho este trazado en color rojo (puede ser cualquier otro que lo diferencie del negro), lo moví a otra área de trazado, con lo que obtuve un dibujo vectorial (propio de un dibujo CAD) partiendo de una imagen .jpg (ver Fig. 7); con él, es posible medirlo, modificarlo, escalarlo, etc., para adaptarlo a las dimensiones señaladas en la Fig. 3.

Fig. 7

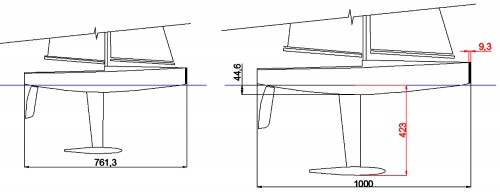
Concretamente, la magnitud de la eslora de este trazado fue de 761,3 mm (podría haber sido otra, dependiendo del tamaño de la imagen .jpg), como se ve en la Fig. 8, por lo que escalé el dibujo para transformarla en otra de 1000 mm, operación que no reviste dificultad (ver Fig. 9).

Fig. 8

Fig. 9

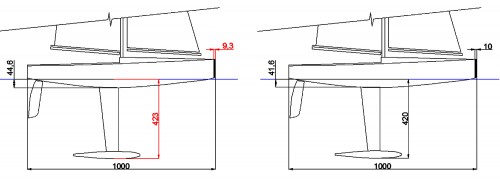
El trazado derecho de la Fig. 9, confirma la bondad del método seguido para llegar hasta él, pues las cotas rojas solo se van de lo permitido en la Fig. 3, en 3 mm para la cota de 423 mm, y en 0,7 mm para la de 9,3, algo que corregí rápidamente y sin esfuerzo, (ver Fig. 10).

Fig. 10

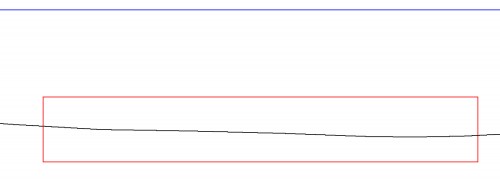
Para facilitar la comprensión de los trazados que siguen, eliminé del dibujo del casco la quilla y el timón, y después comprobé el correcto trazado de cada una de sus líneas, operación conocida con el nombre de corrección de líneas (para esta operación recomiendo leer lo que escribí en la dirección de Internet http://ganandobarlovento.es/diseno-naval-iniciacion/ ). De esta comprobación, que realicé haciendo un gran zoom, – para una perfección mayor, aconsejo imprimir el dibujo a escala 1/1, o mayor, y una ojeada a lo largo de la línea comprobada, denotara enseguida donde ésta hace un quiebro anómalo – detecté que un tramo de la línea que define la parte inferior del casco presentaba una anómala comba, señalada con un rectángulo en la Fig. 11, cuya área está ampliada en la Fig. 12 para evidenciarla.

Fig. 11

Fig. 12

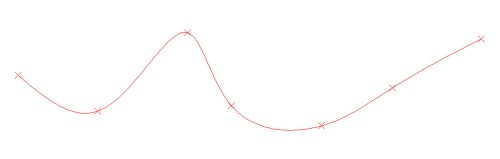
Aunque estas combas sean muy pequeñas, es imprescindible corregirlas, pues dan origen a inaceptables oquedades, depresiones o efectos inversos, en los modelos, que obligaran al modelista a emplastecer, lijar o ambas cosas, más veces de lo conveniente. Debido a esto, no me cansaré de repetir la importancia que tiene la «corrección de líneas», concepto que aplicare a todas las líneas sucesivas que trace. Veamos ahora como se hace esta operación, pero antes aclararé lo que es una línea «spline», tipo de línea que utilizo ampliamente cuando diseño modelos, pues me gustan los que son estilizados, airosos y elegantes, en los que escasean las líneas rectas y las circunferencias. Para ello me referiré a la Fig. 13 (una captura de pantalla del programa CAD que utilizo), en la que están trazados 7 puntos, por los que haré pasar una línea valiéndome del comando «spline» del programa; el resultado de esta operación es lo que se ve en la Fig. 14: una línea «spline», cuya propiedad más característica es su suavidad, pues, en ninguno de sus puntos existen cambios bruscos de su dirección, algo muy própio de todo barco y consustancial con él.

Fig. 13

Fig. 14

Las «splines» informáticas tienen adicionalmente una propiedad inestimable consistente en poderlas cambiar de cualquier punto por el que pasan con gran facilidad, y sin necesidad de borrarlas ni de volverlas a trazar de nuevo.
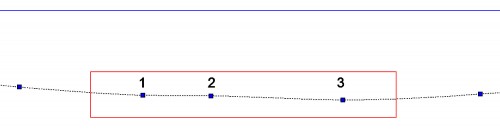
Vuelvo de nuevo a nuestro IOM para decir que la línea señalada con el rectángulo de las Fig. 11 y 12 es una «spline», y al hacer “clic” sobre ella, pasa de ser continua a ser puntos y, además, se quedan marcados con un cuadradito azul los puntos por donde la hice pasar (ver Fig. 15, que es la misma Fig. 12 tras hacer el “clic” antedicho, excepto los números, claro).

Fig. 15

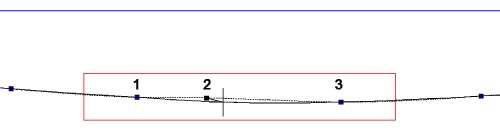
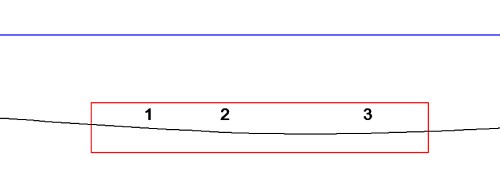
Al volver a hacer “clic” sobre uno de los cuadraditos azules, cambia de color y, además, la «spline» se “pega” al puntero, de modo que la línea se mueve hacia donde vaya el puntero. Concretamente, al pulsar el punto 2 de la Fig. 16, es posible desplazar la línea por debajo de la posición en la que estaba. Al volver a hacer “clic”, la «spline» se fija en su nueva posición, pero sigue siendo de puntos y con cuadraditos azules; de esta condición se sale pulsando la tecla «esc» (ver Fig. 17), con lo que la línea queda bastante ajustada para evitar una hendidura durante la construcción del modelo. Al repetir este mismo proceso con el punto 1 (aunque su desplazamiento fue apreciablemente menor), la línea quedó con un perfil completamente correcto. Como ya he dicho, la máxima perfección de esta corrección de líneas (si la pantalla del ordenador no es suficientemente grande), se consigue imprimiéndolas a escala 1/1, comprobando sus desviaciones y, posteriormente, introduciendo éstas en el ordenador. Más adelante, veremos esto con más detalle.

Fig. 16

Fig. 17

Llegado aquí, y con un alzado del IOM satisfactorio, pasaré ahora a definir el contorno de su planta – normalmente, es el que podríamos ver cuando se mira su cubierta desde una aeronave situada en su vertical y flotando el IOM en aguas tranquilas – de la que el documento «International One Metre. Class Rules 2013» no hace ninguna referencia directa y, en consecuencia, recurrí a buscar una de las muchas que se encuentran en la Red, obviamente en imagen. Entre todas las que vi, elegí la de la Fig. 18 (es solo la mitad), simplemente porque me gustó. Así pues, la manipulé exactamente lo mismo que hice con el alzado logrando así su dibujo vectorial (ver Fig. 19).

Fig. 18

Fig. 19

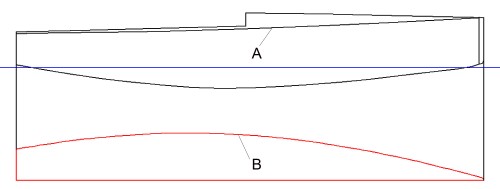
Como se ve en la Fig. 19, su longitud es mucho mayor que los 1000 mm de la eslora de un IOM, por lo que procedí a escalarlo de la manera que ya explique para el alzado, hecho lo cual, situé en la pantalla del ordenador el alzado y la planta de nuestro IOM de la manera que se ve en la Fig. 20; en ella se ve que la longitud de amabas vistas es idéntica, pues las rectas que pasan por sus extremos son paralelas y perpendiculares a la línea roja recta inferior de la planta del ION; esta línea es la que va desde su proa hasta su popa, dividiéndolo longitudinalmente en dos partes iguales y simétricas y es conocida, en cualquier embarcación, con el nombre de «línea de crujía». Añado que, convencionalmente, es costumbre trazar el plano de formas con la proa hacia la derecha y dibujar solamente la mitad de babor de la planta del barco representado, aunque en esto, como en otras cosas, también hay otras costumbres tan académicas como esta. Antes de continuar, insisto de nuevo sobre la necesidad de hacer corrección de líneas, por lo que también en la planta he efectuado esta tarea, siguiendo idéntico método al ya explicado. Adicionalmente, he eliminado del alzado el relleno obscuro de su proa (representaba el material elástico), pues en un plano de formas solo deben existir líneas, algunos números y letras, además de ciertos símbolos, y no otra cosa. Llamo la atención de que la línea “A”, visible en el alzado, representa lo mismo que la “B” visible en la planta, ambas, por tanto, representan a una línea real del IOM que, no es otra, que la línea de unión del costado con la cubierta. Para no complicar el dibujo más de lo conveniente, se suele dibujar solamente la mitad de la planta del barco, dado que la otra mitad es su simétrica; tal es el caso de la Fig. 20.

Fig. 20

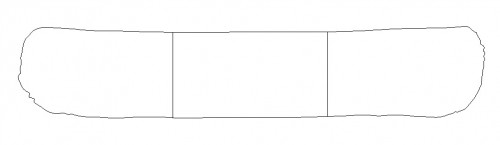
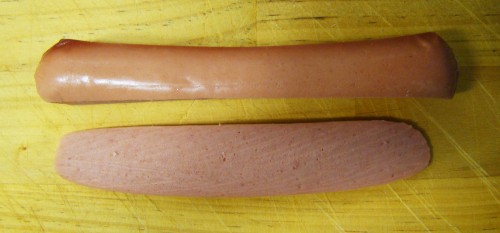
Para una mejor comprensión de lo que sigue, recomiendo una vez más, leer lo que escribí en http://ganandobarlovento.es/diseno-naval-iniciacion/ , no obstante, insisto ahora sobre ciertos conceptos para lo que me valdré de una salchicha – si, de una salchicha, aunque produzca hilaridad -. La Fig. 21, es la fotografía de una salchicha, de la que he hecho, por el método ya explicado, el dibujo vectorial de su contorno, que se ve en la Fig. 22. Con un cuchillo partí la salchicha en tres trozos, procurando que el corte del cuchillo fuera perpendicular a la base en la que aquella se encuentra, como se ve en las Fig 23 y 24.

Fig. 21

Fig. 22

Fig 23

Fig 24

Como se ve en la Fig. 24, los cortes de la salchicha son dos líneas rectas, que, llevadas a nuestro dibujo vectorial de la Fig. 22, se ven como en la Fig. 25.

Fig. 25

Sin embargo, y como sabemos, estos mismos cortes vistos de frente se ven de otra forma, como lo atestigua la Fig. 26. También de este corte he hecho un dibujo vectorial (siguiendo el método ya explicado), como se ve en la Fig. 27, en el que, además, como ya he explicado anteriormente, he igualado (obviamente, son iguales sus longitudes), escalando, la longitud del corte derecho de la Fig. 25 con la longitud vertical de su sección (ver Fig. 27).

Fig. 26

Fig. 27

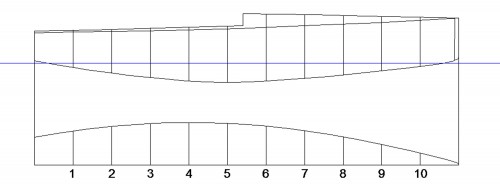
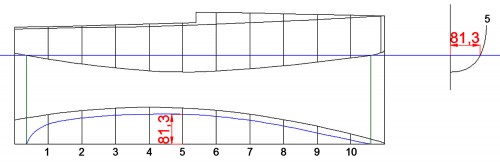
¿Y para qué he explicado esta teoría de la salchicha?, pues para hacer con nuestro IOM lo mismo que he hecho con ella, pues lo “cortaré” en once partes iguales (en vez de tres), como se ve en la Fig. 28, que es el dibujo equivalente al de la Fig. 27, pero el “troceado” lo he hecho sobre el dibujo de la Fig. 20. Observe el lector que, la planta de nuestro IOM, también ha quedado “troceada” en las mismas partes. Esas líneas que representan los cortes que le he dado al modelo, se conocen con el nombre de «cuadernas de trazado» (10, en este caso), de las que seguidamente elegiré la de mayor dimensión de todas ellas, que se conoce con el nombre de «cuaderna maestra» y suele estar situada en el entorno de la mitad de la eslora. Si nos fijamos, la cuaderna 5 está situada exactamente en la mitad de la eslora de nuestro IOM y, hasta la línea de cubierta, es la de mayor altura, pero tiene menos manga que la 4 (manga es la anchura máxima de la cuaderna completa), no obstante, la consideraré como maestra, aunque en puridad no lo sea.

Fig. 28

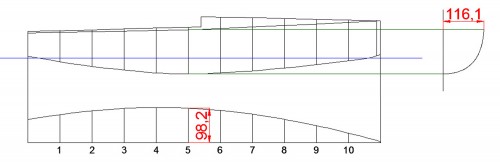
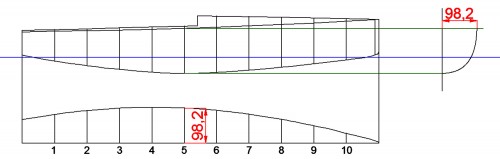
El documento «International One Metre. Class Rules 2013» tampoco impone limitaciones a ninguna cuaderna, de manera que, al igual que hice con la planta, elegí, de la misma manera que hice con el alzado y la planta, una que me gustó. La elegida como cuaderna 5, que posteriormente trace y escalé en altura, del modo ya conocido, es la que se ve en la equina superior derecha de la Fig. 29; pero su semimanga máxima (116.1 mm) supera a la que tiene en planta (98.2 mm), lo que obliga a redefinir su trazado o el de la planta. Por comodidad decidí modificar la cuaderna – debe quedar claro que pueden existir otras razones mucho más técnicas que aconsejen modificar la planta, aunque ahora no analizaré esta cuestión –. Así pues, procedí a la corrección del trazado de la cuaderna, pero no a base de escalarla en semimanga, si no por el método ya explicado de corrección de líneas, resultado de lo cual es el dibujo de la Fig. 30.

Fig. 29

Fig. 30

Las cotas que he puesto en la Fig. 30 y en otras, son solo para facilitar las explicaciones; la línea azul se conoce con el nombre de «línea de flotación» y representa la línea de contacto de la superficie del agua con el casco del barco, cuando éste flota en su condición normal, se representa con las siglas FL, y debe prolongarse hasta las cuadernas, como se ve en el dibujo.
Antes de abordar el trazado en planta de la línea de flotación, vuelvo de nuevo a la socorrida salchicha. Supongamos que nuestra amiga fuese capaz de flotar en el agua, y se sumergiera en ella justo hasta el sitio donde se encuentra el cuchillo que se ve en la Fig. 31; en esa posición del cuchillo, cortamos la salchicha, dando lugar a la sección de corte que se ve en la Fig. 32. ¿Qué significa esto?: que el contorno de esa sección, sería el que tendría su línea de flotación en esa condición. Exactamente haré con nuestro IOM, con la diferencia de que la salchicha existe y aquel todavía no, por lo que tendré que efectuar la operación en sentido contrario.

Fig. 31

Fig. 32

Dicho lo cual, trazaré ahora la línea de flotación sobre la planta que, por el momento, debe pasar inexorablemente por los tres puntos que en este momento ya conocemos: el punto de intersección con la cuaderna 5 y los dos puntos de intersección con la quilla del barco (línea inferior del alzado). El primero está situado a 81.3 mm de la línea de crujía (hago notar que la línea recta vertical de la que arranca la cuaderna 5, es también la línea de crujía, pues divide las cuadernas en dos partes iguales y simétricas) y los otros dos se determinan trazando perpendiculares a la línea de crujía de la planta desde los puntos de intersección de la FL con la quilla, como se ve en la Fig. 33. La línea azul que se ve en la planta, cumple los tres requisitos, pero adelanto ya que, salvo esos tres puntos, los demás los tracé “a ojo” – pero con corrección de línea -, valiéndome de lo que creí más apropiado para lograr un casco esbelto (en este caso, la experiencia juega un positivo papel), por lo que, a buen seguro, sufrirá cambios.

Fig. 33

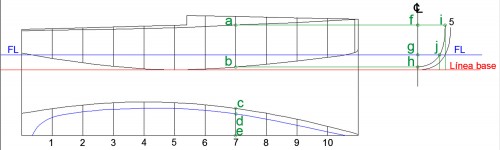
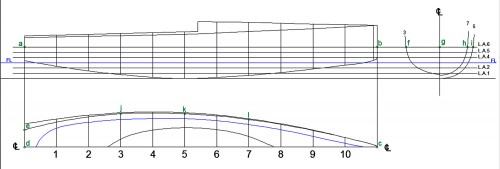
Paso a trazar la cuderna 7 (podría ser cualquier otra), de la que ya conozaco (ver Fig. 34):
– su altura, que es la distancia entre los puntos “a” y “b” (los pequeños circulos, sirven únicamente para señalar los puntos – ahora y en lo sucesivo -, para que sea más eficaz la explicación).
– la semimanga (y obviamente la manga) en su parte superior (en la línea de unión con la cubierta), que es la distancia entre los puntos “e” y “c”.
– la semimanga en la línea de flotación, que es la distancia entre los puntos “e” y “d”.
En consecuencia transferiré estos valores al mismo sitio de trazadado de la cuaderna 7, o sea: la distancia “a” “b”, mediante las dos paralelas color verde que salen de ellos, de modo que al punto “b” le corresponde el “h” (punto de la quilla donde se inicia la cuaderna), y para conocer cual es el punto correspondiente del “a”, tracé una paralela (también en color verde) a una distancia a la línea de crujía igual a la distancia de “c” a “e”, que se corta con la línea verde trazada desde “a”, en el punto “i”. Así pues, en este momento ya tengo dos puntos de la cuaderna 7; su semimanga en la línea de flotación, es la distancia de “d” a “e”, por lo tanto, la cuaderna debe tener esta misma medida en el lugar de trazado de la forma de las cuadernas (trazado derecho del dibujo), por lo que vuelvo a trazar a la distancia “d” “e” una paralela a la línea de crujía (en verde), la cual corta a la línea de flotación en el punto “j” (“d” “e” = “g” “j”), con lo que ya puedo trazar la «spline» de la cuaderna 7, algo que ya está hecho en el dibujo. Salvo la cuaderna maestra (en este caso, la 5) que no deberá sufrir niguna modificación, todas las demás trazadas, como acabo de explicar, es muy normal que deban someterse al método de corrección de líneas, a medida que progrese el plano.

Fig. 34

La línea horizontal que, normalmente, pasa por el punto más bajo del barco, se llama «línea base» (en este caso, de color rojo – los colores los pongo solo para facilitar las explicaciones -); el área de cualquier plano de formas donde están trazadas las formas (valga la redundancia) de todas las cuadernas, se llama «caja de cuadernas», en ella es normal que la cuaderna maestra se dibuje completa y solo se dibujen, a la derecha de la línea de crujía, las mitades de las cuadernas comprendidas entre la maestra y la proa y, a la izquierda, el resto. Finalmente, diré que la línea de crujía se identifica con este símbolo:

.
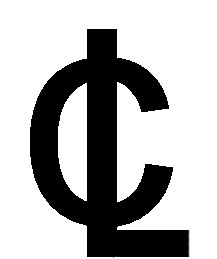Para continuar, he trazado varias líneas paralelas a la de flotación que, además, son equidistantes entre sí, y las he marcado como L.A.1, L.A.2, L.A.4, L.A.5 y L.A.6. Estas líneas, conocidas con el nombre de «líneas de agua» se definen de la misma manera que lo ya explicado para la línea de flotación, o sea, la número 1 sería la FL si el barco flotara normalmente en esa condición; la número 2 sería la FL si el barco flotara de esa manera, y así sucesivamente; así pues, la línea de flotación es la línea de agua en la que el barco (IOM) flotara cuando esté terminado. Dicho esto, trazaré ahora la línea de agua 1, de la que tengo ya cuatro puntos conocidos:
– Los dos de su corte con la quilla, que he transferido a la planta mediante las dos rectas perpendiculares a la línea de crujía (en color verde).
– Los dos de su corte con las cuadernas 5 y 7, y por lo tanto la longitud de sus semimangas: de “a” a “b” para la cuaderna 7, y de “a” a “c” para la cuaderna 5. Estas longitudes se transfieren a las mismas cuadernas de la planta, de modo que: longitud “e” “d” = longitud “a” “c” y longitud “g” “f” = longitud “a” “b”.
Hecho esto tracé, corrigiéndola, la spline que representa la línea de agua 1 (en lo sucesivo, a cualquiera de ellas, las citaré como L.A.), como se ve en la Fig. 36. Con respecto a esta L.A., debo decir lo mismo que para la cuaderna 7: casi con toda seguridad, será necesario modificarla; más adelante lo veremos.

Fig. 36

Trazaré ahora la cuaderna 3, para lo que haré referencia a la Fig. 37. En este momento conozco de ella lo siguiente:
– su altura: distancia de “e” a “f”, la cual la transferiré al la caja de cuadernas, trazando por dichos puntos las dos paralelas (en verde) a las L.A. La que pasa por “e”, determina el punto “h” en su corte con la línea de crujía de la caja de cuadernas, que define el punto más bajo de la cuaderna. El punto “f” lo transferí a la caja de cuadernas, simplemente haciendo “m” “l” = “a” “d”.
– siguiendo este mismo criterio anterior, hice que “j” “k” = “a” “c” y “h” “i” = “a” “b”
con ello he definido cuatro puntos de la cuaderna 3, “g”, “i”, “k” y “m”, por los que hice pasar la spline que define el contorno de la cuaderna 3.

Fig. 37

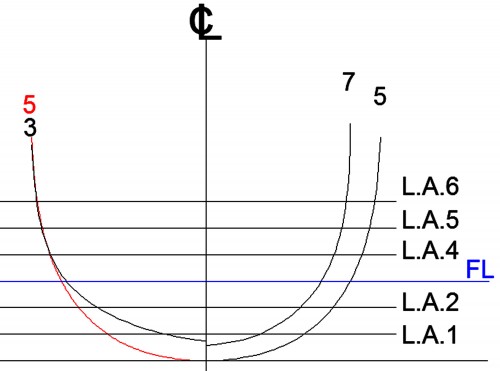
En este momento, y haciendo zoom, la caja de cuadernas se encuentra tal como se ve en la Fig. 38 – pongo en color rojo la cuaderna 5 para diferenciarla de la 3, en la zona de superposición de ambas -; esta superposición no me parece nada normal, pues están bastante distanciadas entre sí y, como es obvio, la mayoría de los barcos – por no decir todos – se afinan (se estrechan) hacia su popa y proa y, sobre todo, de sus partes altas a las bajas.

Fig. 38

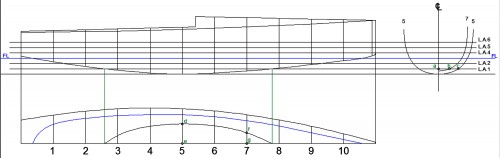
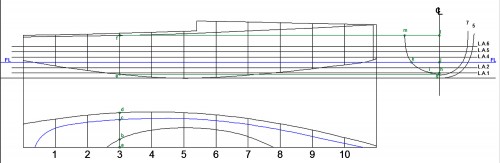
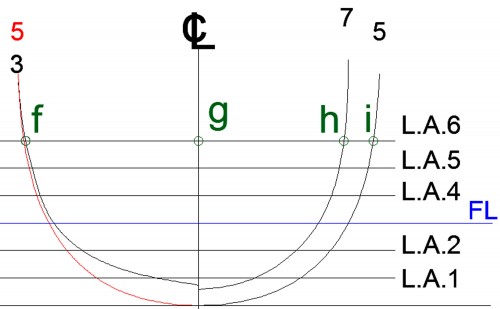
Para comprobar la existencia o no de la anormalidad antedicha, tracé en planta la L.A.6, trazado que, a estas alturas, cualquier lector podría hacer, no obstante, y para fijar definitivamente los conceptos, volveré a repetirlo (ver Fig. 39):
– La L.A.6 corta al contorno del alzado del IOM en los puntos “a” y “b”; este último, es en el de cruce del tramo de estribor con el tramo de babor de ésta línea; pertenece por tanto a la línea de crujía, pues solo él es simétrico de sí mismo, en consecuencia, su correspondiente en planta es el punto “c”. En este momento es una indefinición el correspondiente en planta del punto “a”, por lo que he decidido, tras visionar fotografías de estos modelos, que su semimanga sea “d” “e”. También habría podido localizar en Internet una imagen de su espejo (para quien no lo sepa, recibe este nombre aquella superficie que cierra por popa el casco de un barco – la cuaderna “0” de la Fig. 43 -) o, mejor aún, el trazado del mismo, y proceder con ellas de la manera ya explicada, pero he decidido hacerlo así por ser más ilustrativo.
– La L.A.6 tiene las siguientes semimangas: en la cuaderna 3 la “g” “f”; en la cuaderna 5 la “g” “i”, y el al cuaderna 7 la “g” “h”. En consecuencia, tracé en planta y sobre estas cuadernas los puntos “j”, “k” y “l”, de modo que: desde “j” hasta crujía = “g” “f”; desde “k” hasta crujía = “g” “i” y desde “l” hasta crujía = “g” “h”.
Los puntos “e”, “j”, “k”, “l” y “c”, son por los que debe pasar la L.A.6, como se ve en la Fig. 39

Fig. 39

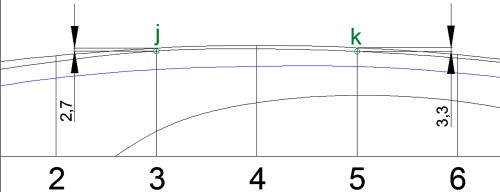
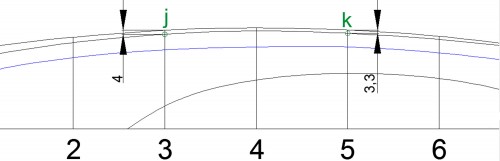
Aparentemente, la L.A.6 ha salido con una forma aparentemente muy aceptable, pero en el zoom de la Fig. 40 se observa que en la cuaderna 3 su distancia a la línea de cubierta o, lo que es lo mismo, a la línea que pasa por los puntos más altos de las cuadernas, es de 2.7 mm, mientras que esta misma distancia para la cuaderna 5 es de 3.3 mm, algo inaceptable, pues he dicho anteriormente que todos o casi todos los barcos afinan hacia popa, proa y desde su parte alta a la baja, condición incumplida en este caso, pues lejos de afinar, engorda. Si esto quedase así, el casco exhibiría un impropio abultamiento en esa zona de la cuaderna 3; en consecuencia, procede:
1º – corregir la L.A.6 en la cuaderna 3 y, si ello no es suficiente, corregirla también en las cuadernas circundantes, pero no en la 5 ni en la 7 (por ahora).
2º – corregir la cuaderna 3 para que su semimanga con la L.A.6, sea la misma de ésta tras su corrección; si fuese necesario corregir alguna otra de su semimanga en la FL, también deberá corregirse ésta. En resumen, todas las semimangas de la caja de cuadernas deberán ser idénticas a sus correspondientes en planta, aunque para ello sea necesario hacer todas cuantas correcciones sean necesarias.

Fig. 40

Hechas las correcciones antedichas, la L.A.6 ha quedado como se ve en la Fig. 41 y la cuaderna 3 como se ve en la Fig. 42, en la que he vuelto a situar la parte simétrica de la cuaderna 5 (en rojo) para que se pueda observar su diferencia con la Fig. 38. Pese a esta corrección, no se puede descartar alguna más, a medida que progrese el plano de formas, de esta y otras cuadernas y líneas de agua, de modo que, éste, junto con la corrección de líneas, es el trabajo fundamental de quien se decida a trazar un plano de formas fetén siguiendo este método.

Fig. 41

Fig. 42

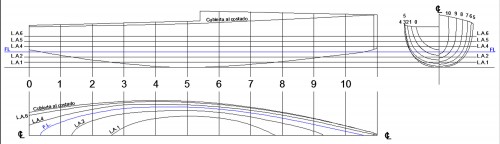
Después de algún tiempo, paciencia y algunas correcciones, di por terminado el plano, de la Fig. 43; en él es posible apreciar modificaciones de algunas líneas, como por ejemplo la L.A.6. Con objeto de no complicar más el plano, ni he hecho el trazado de la L.A.5, ni el de otras líneas de agua por encima de la L.A.6; también he puesto nombre a cuadernas, L.A. y a alguna línea fundamental. Para simplificar, me he abstenido de describir el trazado de longitudinales y diagonales pues, para un modelo, creo suficiente lo ya explicado; también he prescindido del trazado de la cubierta del IOM, algo que dejo para quien guste de probar los conocimientos adquiridos tras la lectura de este texto.

Fig. 43

Finalmente deseo decir que, aunque lo pueda parecer, no es éste un trazado complicado, y debe verse bajo el prisma – por poner un ejemplo – de quien, durante su aprendizaje para andar en “bici”, lo ve como algo complicadísimo, y una vez que aprendió, le parece algo tirado. Destaco también que, el trazado del plano de formas de un modelo hecho por quien lo va a construir, da a éste todas las posibilidades de imprimir en ellos su propia personalidad, algo difícil en otro caso.
Deseo suerte a todo modelista que, tras haber tenido la paciencia de leer este texto, se embarque en el trazado de un modelo, y descubra con satisfacción lo entretenido que es esta faceta como proyectista.
Página principal:

http://ganandobarlovento.es/