Diseño naval: iniciación

Como ya he dicho en otro escrito de este blog, una de mis grandes aficiones es diseñar y construir modelos de barcos. Probablemente y debido a ello, algunos modelistas navales me han pedido en alguna ocasión que les enseñara dibujo naval, más concretamente la confección de planos de formas. Adicionalmente, también he visto en algunas páginas de la Red, a algunos de estos excelentes modelistas exponiendo con legítimo orgullo sus magníficos trabajos, pero he notado en bastantes de ellos un desconocimiento casi total del dibujo naval, que han soslayado realizando algunos tediosos aunque espléndidos trabajos que, en más de una ocasión, me han dejado con la boca abierta, a tenor de los resultados logrados. Por todo ello – y porque un jubilado, como yo, dispone del tiempo necesario para abordar ciertos problemas, otrora inabordables – he tomado la decisión de explicar aquí los rudimentos básicos para la confección de planos de formas de barcos, aún a sabiendas de que tal decisión entrañará para mi algunas dificultades, considerando que fue el año 1.964 la última vez que tuve contacto con la geometría descriptiva teórica… ¡pero lo intentare! Deseo aclarar también que el método que seguiré para explicar sus conceptos básicos, podrá parecer un tanto cutre y salchichero (como diría un conocido presentador de TV), dado los enormes recursos didácticos que a día de hoy brinda la informática, pero aclaro que lo que sigue no es más que la suma de una exposición de los elementales medios de que dispongo para llevar a cabo este proyecto y, de un enorme deseo de que lo que aquí explico pueda ser útil para alguno de mis admirados y desconocidos modelistas navales que deseen adquirir estos conocimientos; para todos ellos, van dirigidas estas líneas.

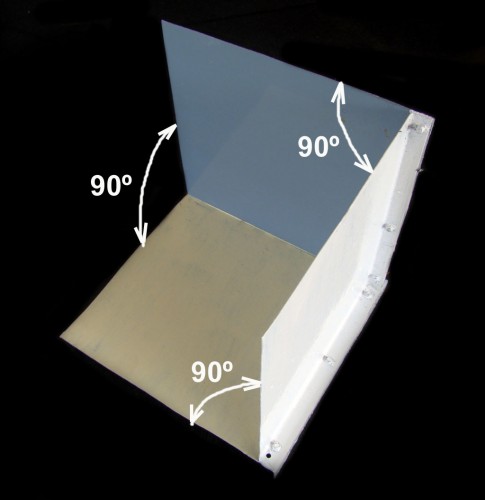
Antes de nada deseo decir que, quien lea este texto, debe dominar con soltura los conceptos de perpendicularidad, paralelismo y simetría. Dicho lo cual, empezare presentando al lector un pequeño y elemental artilugio – así lo llamare en lo sucesivo – formado por tres trozos de chapa de acero – de la utilizada en estanterías metálicas – que he unido entre sí, de forma que cada dos de ellas formen un ángulo de 90º, tal como se ve en la Fig. 1; como consecuencia de ello, también forman ángulo de 90º las líneas de unión de las chapas, como se ve en la Fig. 2. Seguidamente pondré nombre a las caras interiores del artilugio, a las que he llamado plano “1”, “2” y “3” – así… de forma “poco académica” – pero perfectamente comprensible; a todas ellas las he pintado de distintos colores para potenciar el efecto de relieve sobre las fotografías  (ver Fig. 3).

Fig. 1

Fig. 2

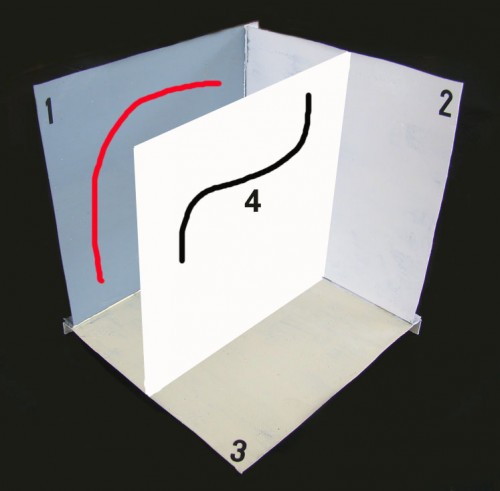
Fig. 3

Hecha la presentación del artilugio, alguien podría preguntar con toda la razón ¿que tiene que ver este “invento” con el dibujo naval? y, aunque parezca increíble, la respuesta es: ¡mucho! pues me valdré de él con el objetivo de que ciertos conceptos sean más fácilmente comprendidos por aquel lector que tenga la paciencia de leer un tema tan árido en su lectura como eficaz en sus resultados.

También hare uso de un lápiz afilado por ambos extremos, al que he soportado con una fina varilla de acero de coloración rosa, a su vez, unida a una pequeña chapita de acero, de modo que todo el conjunto se adhiera al artilugio mediante un pequeño imán (ver Fig. 4). Advierto que en las fotografías que siguen, he eliminado (con más o menos éxito) este soporte, con objeto de que no interfiera con las explicaciones.

Fig. 4

Este lápiz, visto ahora en la Fig. 5, tiene 122 mm de longitud (esa es la única razón de la presencia del metro) y lo utilizare como materialización de la línea recta (la línea azul) que va de una punta del lápiz a la otra.

Fig. 5

Adicionalmente también he tomado la vista del lápiz en la dirección del plano 3 (ver Fig. 6). De las infinitas líneas rectas que se pueden trazar desde la punta izquierda del lápiz hasta el plano “1”, solo he trazado la única que forma un ángulo de 90º – sea cual sea la dirección en que se mida – en el punto de intersección con él, de modo que la longitud “d”, que va desde la punta del lápiz hasta el punto de intersección de esta recta con el plano “1”, es la distancia de la punta del lápiz hasta este plano; este concepto es idéntico para cualquier otro punto y para cualquier otro plano.

Fig. 6

He utilizado los dos metros que se ven en la Fig. 7, para constatar que la distancia de ambas puntas del lápiz hasta el plano “1” es de 76 mm (deseo aclarar que ni en esta fotografía ni en ninguna otra – especialmente cuando están tomadas muy próximas al objeto a fotografiar – se captan las distancias en su longitud real); esta condición convierte a la línea recta imaginaria que une las puntas del lápiz (la línea azul) en paralela al plano “1”, de lo que se deduce que para que una línea recta sea paralela a un plano, es condición imprescindible que dos puntos cualquiera de la misma (en este caso, las dos puntas del lápiz) deben estar a la misma distancia del plano.

 Fig. 7

Veamos ahora la línea L que he trazado de una a otra punta del lápiz en la Fig. 8; salta a la vista que, excepto los dos puntos de sus extremos (las puntas del lápiz), todos los demás están a una distancia del plano “1” mayor de 76 mm, lo que automáticamente la convierte en una línea NO paralela a este plano; de lo que se deduce que para que una línea no recta sea paralela a un plano, todos sus puntos deben estar a la misma distancia de él.

Fig. 8

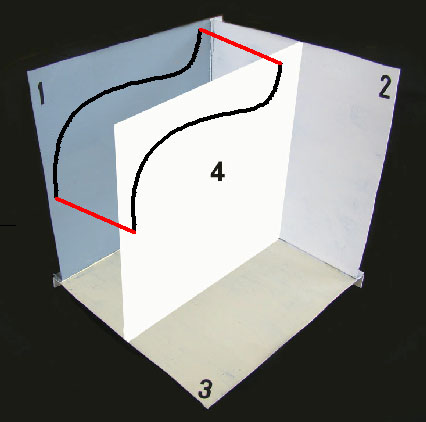
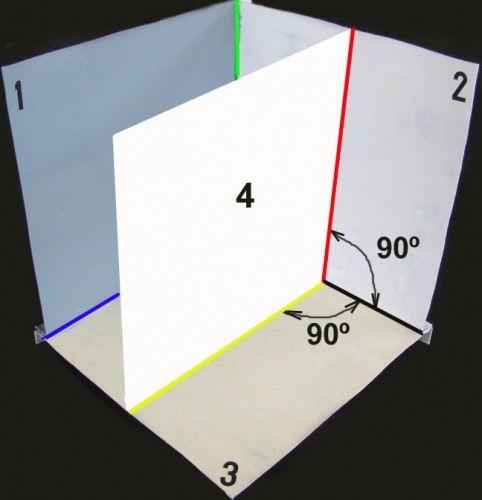
Veamos ahora la Fig. 9. En ella he añadido al artilugio el plano “4”, al que le he impuesto la condición de que todos sus puntos estén a la misma distancia del plano ”1”, condición ésta que automáticamente lo convierte en paralelo a él; por lo tanto, para que dos planos sean paralelos todos los puntos de uno deben estar a la misma distancia del otro, de lo que también se deduce que todas las líneas – rectas o no – que se tracen sobre uno de ellosserán, automáticamente, paralelas al otro. La línea negra de la Fig. 9a, está trazada sobre el plano “4”, por lo tanto es paralela al plano “1”; de la misma manera, la línea roja está trazada sobre el plano “1”, lo que la convierte en paralela al plano “4”. Cualquier línea contenida en un plano paralelo a otro, se proyecta sobre éste con sus mismas dimensiones y formas (ver Fig. 9b).

Fig. 9

Fig. 9a

Fig. 9b

Llegados aquí, creo que ya hemos adquirido los conocimientos mínimos imprescindibles para poder analizar cómo se proyectan los elementos geométricos situados en el espacio sobre  determinados planos, concretamente sobre los tres planos que forman nuestro conocido artilugio. También quiero hacer hincapié que la proyección geométrica – clave de lo que aquí trato de explicar –  es idéntica a la formación de sombras solares (*), siempre que los rayos solares sean perpendiculares al plano donde se formen las sombras de los elementos geométricos en cuestión.

(*) Los rayos solares tienen la propiedad de ser paralelos, de ahí que los utilice para la proyección de sombras, en vez de otro tipo de luz cuya emisión podría ser en forma de rayos divergentes, como es el caso de la luz emitida por las lámparas incandescentes, por poner solo un ejemplo.

Dicho lo cual, pasare ahora a analizar lo que ocurre cuando se proyectan sombras solares sobre los distintos planos del “afamado” artilugio. La Fig. 10 está tomada cuando la línea azul que une las dos puntas del lápiz es paralela al plano “1” (las distancias “a” de ambas puntas, por tanto, son iguales y de 76 mm, como vimos en la Fig. 7) y los rayos del sol inciden perpendicularmente sobre él (de la misma manera que lo explicado en la Fig. 6) formándose la sombra proyectada por el lápiz; esta proyección es exactamente igual que una proyección geométrica, como ya he dicho antes. De esta observación también se deduce que las puntas del lápiz, se proyectan sobre el plano como puntas, lo que no deja ninguna duda de que la proyección geométrica de un punto sobre cualquier plano, es otro punto.

Fig. 10

Se aprecia por la regla metálica graduada en mm de la Fig. 10, que la recta blanca que une los extremos de la sombra del lápiz, tiene la misma longitud que la recta azul que une las puntas del lápiz (122 mm, como ya quedo dicho en los comentarios a la Fig. 5). Esta característica es propia de las rectas paralelas a un plano, que siempre se proyectan sobre él con su misma longitud, por la razón siguiente: ambas rectas “a” forman un ángulo de 90º con el plano “1” (por la propia definición de distancia de un punto a un plano – ver Fig. 6 – ) y, por lo tanto también, con la sombra del lápiz, con lo que ésta, ambas rectas y el propio lápiz, no tienen ninguna otra posibilidad más que la de formar un paralelogramo que, como sabemos, tienen sus lados opuestos iguales.

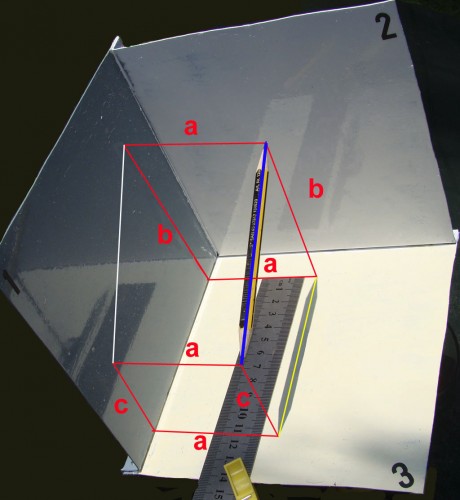
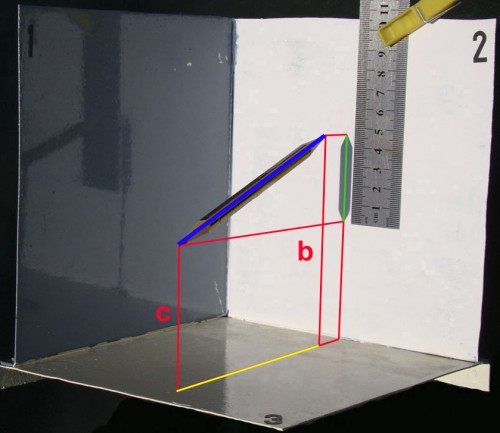
Veamos ahora la proyección del lápiz sobre el plano “3”, para lo cual haremos que los rayos solares incidan ahora perpendicularmente sobre él; pero antes quiero advertir que, en esta ocasión, la recta azul que une los extremos del lápiz no es paralela a dicho plano pues, como se puede apreciar, las distancias “b” y “c” de sus puntas a dicho plano, son diferentes (ver Fig. 11). También la longitud de la recta (medida también con la regla metálica milimetrada) que une los extremos de su sombra (114 mm y de color amarillo), es menor que la longitud de la recta azul (los 122 mm, ya mencionados); lo que confirma lo dicho en el párrafo anterior, o sea que, solo las rectas paralelas a un plano se proyectan sobre él con la misma longitud. Aprovecho esta misma Fig. para incluir en ella los mismos elementos gráficos de la Fig. 10, o sea, la línea blanca (longitud de la sombra proyectada por el lápiz sobre el plano”1”) y las distancias “a”

Fig. 11

La proyección del lápiz sobre el plano “2”, sigue criterios idénticos a los del plano “3”, aunque la proyección de la ya conocida línea azul, o sea, la línea verde, es todavía más corta que su proyección sobre el plano “3” que, como acredita la regla metálica, es de 46 mm

Fig. 12

Llegados aquí alguien, no sin razón, puede preguntar: y… todo esto ¿para qué? Pues bien, si alguien fijándose en las Fig. 11 y 12 otorgara valores en mm a “b” y “c” y trazara sobre un papel lo que ve en el plano “1” del artilugio, sin ninguna duda el resultado de tal trabajo sería el que se ve en la Fig. 13 y que, seguidamente paso a analizar:

La superficie de color azulado representa al plano “1” y también al papel en el que realizaría el trazado, que comenzaría trazando primeramente la recta “T”, recta que representa la línea de unión de los planos “1” y “3” del artilugio; seguidamente dibujaría una recta perpendicular a ”T” de una longitud “c”; luego trazaría otra, también perpendicular a “T”, pero de longitud “b”, teniendo cuidado de que la distancia entre ambas sea la longitud de la sombra del lápiz sobre el plano “3” (114 mm, como se recordara); finalmente trazaría la recta blanca que une los extremos de estas dos rectas, que si la midiese tendría, ¡seguro! ¡seguro!, una longitud de122 mm, la longitud de nuestra “estrella” el lápiz; siendo ésta, por tanto, la proyección de la recta azul sobre el plano “1”.

Fig. 13

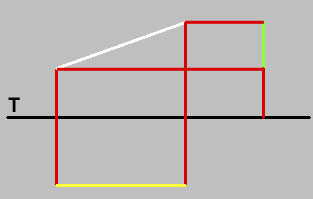
Ahora haremos lo mismo, pero trazando lo que se ve en el plano “3” y con la única diferencia de situar la sombra o proyección del lápiz en la parte inferior de la línea de unión de los planos “1” y “2”, o sea, la misma línea “T” de la Fig. 13. El resultado será el de la Fig. 14, que dejo al lector que la analice por sí mismo, siguiendo los criterios explicados para la Fig. 13.

Fig. 14

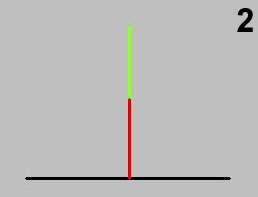
Finalmente haremos el trazado de lo que se ve en el plano “3” pero, en este caso, la línea negra representa la de unión entre los planos “2” y “3” y la línea bicolor es vertical a ella, de la que su parte roja es de longitud “c” y su longitud total es “b”, siendo por tanto la parte verde la longitud de la proyección del lápiz sobre el plano “3”.

Fig. 15

Las tres vistas de las proyecciones del lápiz sobre los tres planos “1”, “2” y “3”, no se trazan cada una por su lado – como he hecho hasta aquí – sino que forman un conjunto único, perfectamente relacionadas entre sí, de modo que a la proyección sobre el plano “1” se conoce con el nombre de alzado, planta a la del plano “3” y, perfil a la del plano “2”. En la Fig. 16 están unidas las tres vistas correspondientes a las Fig. 13, 14 y 15, de modo que la recta blanca es el alzado de la recta azul (la que va de una punta a otra del lápiz), la recta amarilla es su planta y la verde su perfil. Llamo la atención del lector para que observe como el dibujo sobre el plano ”2” está representado como si éste y el plano “1”, se hubieran abierto como un libro sobre la misma superficie. También aclaro que si el lápiz se desplaza paralelamente a sí mismo, la forma y longitud de sus tres vistas no variaran, lo mismo ocurrirá si aquel se desplaza en el plano que lo contiene perpendicular al plano “3”, alejándose o acercándose al plano “2”, lo único que variará, en ambos casos, serán las longitudes de las rectas rojas que, por otro lado, no siempre se representan en los planos. Antes de dar por finalizado este apartado quiero hacer hincapié que, forzosamente, la recta que une los dos puntos que representan el alzado y planta de otro situado en el espacio, debe de formar un ángulo recto (90º) con la línea “T”; de la misma manera, la línea que une dos puntos que representan el alzado y el perfil de otro situado en el espacio, debe ser paralela a la línea “T”. Aconsejo a quien tenga interés en este tema y todavía no esté hasta el gorro de él, que haga un pequeño esfuerzo para comprender perfectamente estos conceptos… son fundamentales.

Fig. 16

Antes de continuar, recalcaré algunos conceptos fundamentales que son básicos para comprender los intríngulis del dibujo naval, tales como:

–       La intersección de dos planos, es una línea recta (la azul, verde, amarilla, negra y roja, del artilugio, visto en la Fig. 17)

–       Las líneas de intersección que forman dos planos paralelos entre sí (el 1 y el 4 de la Fig. 17) con un tercero (el 2 o el 3), son también paralelas (roja y verde, así como azul y amarilla, de la misma Fig.)

–       Las líneas de intersección de un plano perpendicular (4) a otros dos (2 y 3), son también perpendiculares a la línea de intersección (negra) de estos (ver Fig. 17).

Fig. 17

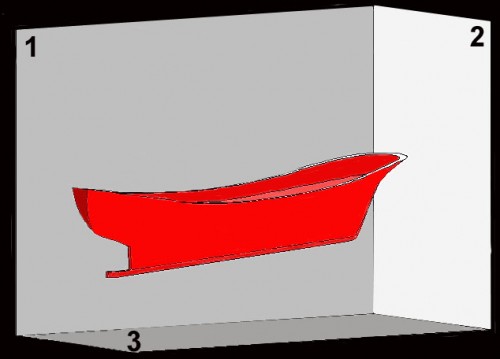
Para explicar ahora dibujo naval, me valdré de un modelo de barco – concretamente, un típico pesquero de madera del Cantábrico – que he diseñado, construido y que muestro en la Fig. 18.

Fig. 18

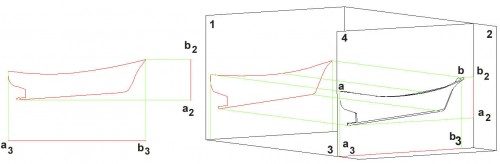
Tal modelo lo situaré ahora en el interior de otro artilugio de características idénticas al que ya conocemos – aunque, en esta ocasión y como puede observarse, solo existe como dibujo – (ver Fig. 19). Para mayor claridad, en los gráficos que le siguen, he eliminado en ellos el timón y la hélice del modelo; también he eliminado el color, tanto a los planos del artilugio como al modelo. También he situado a éste como si flotara normalmente en el agua, de modo que el plano “4” que lo atraviesa de proa a popa – exactamente el que pasa por su parte central dividiéndolo en dos partes perfectamente simétricas, conocido como plano de crujía – sea perpendicular a los planos “2” y “3” y, por tanto, paralelo al “1”, tal como se aprecia en la Fig. 20. En ella, solo he dibujado la mitad derecha del casco (lado de estribor) y también la he alejado paralelamente del plano “1”, con objeto de poder apreciar mejor su proyección sobre él. Las líneas verdes dirigidas hacia el plano “1”, son las de proyección de los puntos del contorno exterior del casco, sobre él; las dirigidas hacia el plano “2”  son las de proyección de los puntos a y b sobre él (los que determinan la eslora máxima del modelo) que dan lugar a los puntos proyectados a₂ y b₂, contenidos en el plano “4”, y las dirigidas hacia el plano “3” son las proyecciones de estos mismos puntos, a y b, sobre él, y que dan lugar a los puntos proyectados a₃ y b₃. Como es obvio, solo he trazado algunas proyecciones de la silueta del casco, para no complicar el dibujo más de lo conveniente. Esta proyección del casco sobre el plano “1” es su alzado, y tiene un tamaño y forma idéntica a la de su silueta. La línea recta roja, proyección de la silueta del casco sobre el plano “3” – la que va desde a₃ a b₃ – es la eslora (longitud) total del barco y la línea roja que va desde a₂ a b₂ es la altura total del mismo. A la izquierda de la representación tridimensional, están trazados el alzado del casco – idéntico a la intersección del plano “4” con él – y la proyección de éste sobre los planos “2” y “3” (note el lector que, a éstas, no las nombro como planta y perfil del casco, pues solo representan una parte mínima de él) .

Fig. 19

Fig. 20

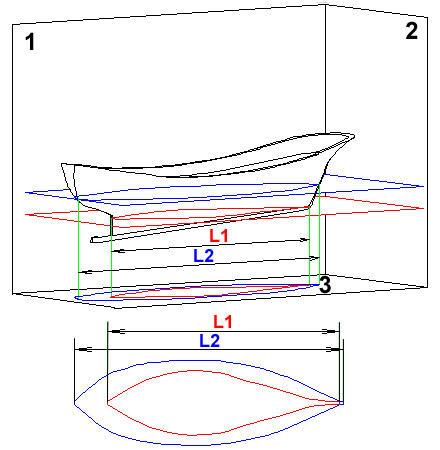
Daré ahora otro paso más, introduciendo en el artilugio otros dos planos más, el azul y el rojo de la Fig. 21; estos dos planos son paralelos entre sí, perpendiculares a los otros planos “1” y “2” y, por lo tanto, paralelos al plano “3” y a la superficie del agua donde hemos supuesto que el barco esta flotando. Estos planos intersecan el barco formando dos líneas cerradas, cuyas proyecciones sobre el plano “3” son de las mismas dimensiones y formas que ellas, que se conocen con el nombre de líneas de agua. En la parte inferior de la Fig. 21 están dibujadas las plantas de ambas líneas de agua (solo de ellas, no del casco completo). Las longitudes L1 y L2 son las correspondientes a las esloras (longitudes) máximas de las dos líneas de agua.

Fig. 21

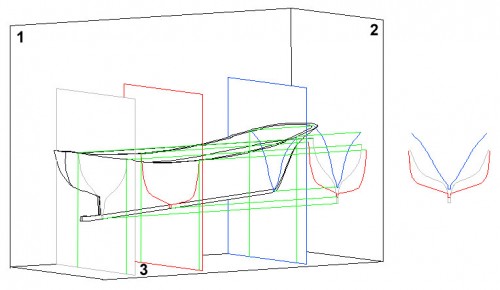
En la Fig. 22 se ven ahora tres nuevos planos – gris, rojo y azul –  paralelos entre sí, perpendiculares a los planos “1” y “3”  de nuestro artilugio y, en consecuencia, paralelos al plano “2”; todos ellos cortan el casco del pesquero en secciones de su mismo color, proyectadas sobre los planos “1” y “3” como rectas (solo representadas las del plano “3” para no complicar el dibujo) y, sobre el plano “2” en sus formas y dimensiones reales que, a la derecha de la Fig. están representadas en su dimensión real. Esta representación es el perfil de estas secciones del casco que, a partir de este momento, vamos a conocer con el nombre de cuadernas de trazado.

Fig. 22

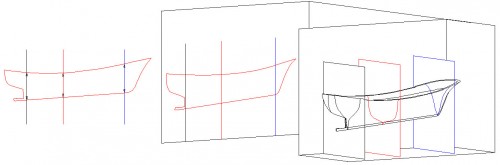
Llegados aquí ya comprendemos como se generan el alzado, planta y perfil del casco de un barco, por lo que, ahora describiré sus relaciones, para lo que en la Fig. 23 (en la que ya no pongo nombres a los planos del artilugio, como hare en lo sucesivo) he combinado las partes de las Fig. 20 y 22 que ilustran la interacción de una con otra, por lo que, en la parte derecha de ella, se ve que los planos gris, rojo y azul y, por ende, las secciones originadas en su intersección con el casco, se proyectan sobre el plano “1” como líneas rectas, haciéndolo además, con sus mismas longitudes; o sea, los tramos de rectas comprendidos entre las puntas de flecha son las alturas reales máximas (técnicamente, puntal máximo de cada cuaderna) de las cuadernas.

Fig. 23

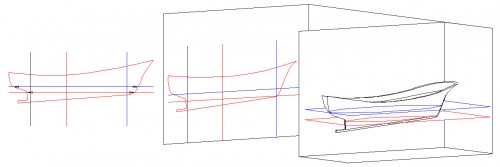
La Fig. 24, combina parte de la Fig. 21 y de la 23. De ella se desprende que, en el alzado del casco se ven, en su tamaño real, las longitudes (esloras) máximas de las líneas de agua, que son los tramos de recta comprendida entre las puntas de las flechas.

Fig. 24

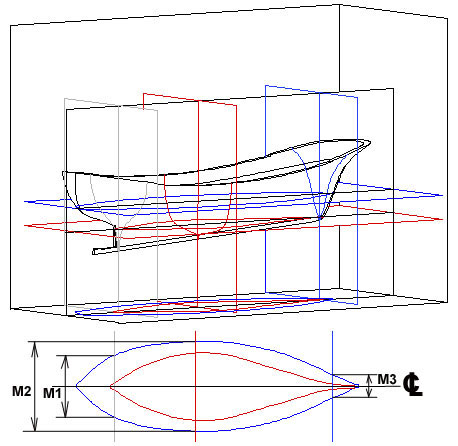
La Fig. 25 combina parte de las Fig. 20, 21 y 22. En ella se ven las dos líneas de agua – ya explicadas – y las intersecciones de los planos gris, rojo y azul de la Fig. 22, con ellas. No es difícil deducir que los segmentos que aquellas interceptan con estas (técnicamentedenominadas: mangas), son las anchuras reales de las cuadernas con esas líneas de agua, de las que solo he señalado las correspondientes a la línea de agua azul (M1, M2 y M3). Señalo también que, la línea negra que divide simétricamente a las dos líneas de agua, corresponde al plano de crujía, del que también he hablado cuando me referí a la Fig. 20, y que está representado en la parte inferior de la Fig. 25 con el símbolo   .

Fig. 25

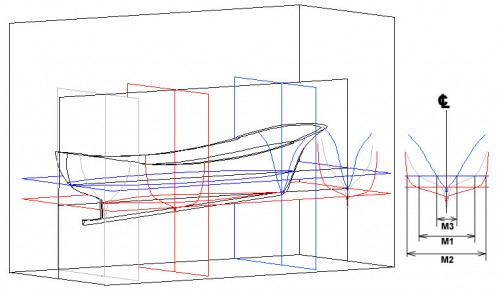
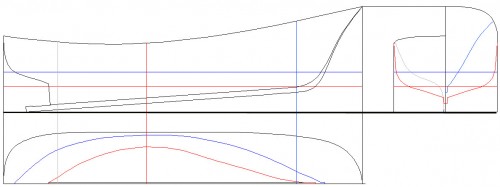
Veamos ahora la Fig. 27 en la que, además de las líneas de agua azul y roja, también está incluido el plano de crujía y, en su parte derecha, vemos las cuadernas de trazado originadas por los planos gris, rojo y azul (ya explicados en la Fig. 22), junto con las líneas de agua y la de crujía. Los segmentos interceptados por las cuadernas con las líneas de agua, son idénticas a las mangas reales del barco tomadas en estos mismos puntos y, además, también son idénticas con las representadas en la planta del casco; de manera que las mangas M1, M2 y M3 que se ven en la Fig. 27 (correspondientes también a la línea de agua azul), son idénticas a las señaladas en la Fig. 25

Fig. 27

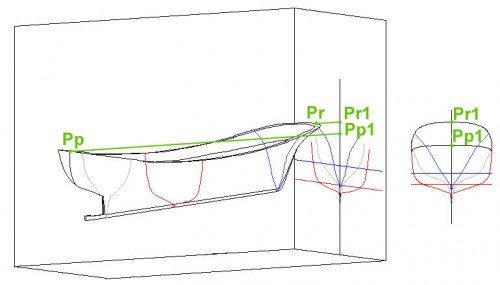
Daremos ahora otro paso más preguntándonos ¿Qué pasa con la línea que define los puntos más altos de las cuadernas del pesquero o, lo que es lo mismo en este caso, la línea de borda? La respuesta está dada en la Fig. 28 (a la que están eliminados todos los planos, excepto el “1”, “2” y “3”), pues esta línea es la que une todos los puntos más altos de las cuadernas y los puntos más extremos de proa y popa – Pr y Pp – del barco que los obtendremos por su proyección sobre el plano “2” (Pr1 y Pp1), o sea, sobre el que contiene todos los trazados de las cuadernas. La parte alta de las líneas negras (parte derecha de la Fig.) representa la parte de proa de la proyección de la borda del barco (desde la cuaderna roja hasta el extremo de proa) y, la línea negra inferior representa la proyección  de la parte de popa de la borda del barco (desde la cuaderna roja hasta el extremo de popa). Note el lector que, para mayor claridad, no están trazadas estas mismas líneas en el plano “2” del artilugio.

Fig. 28

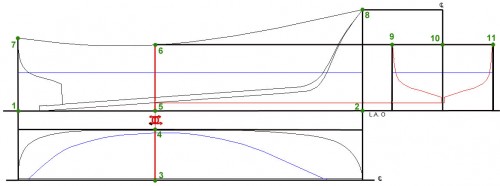
Como se aprecia en las Fig. 25 y 28, las líneas de agua, cuadernas y de borda, están trazadas tanto en su lado de babor (izquierdo) como en el de estribor (derecho) pero, como ya sabemos, todas ellas son simétricas con relación al plano de crujía, motivo por el cual solo se representa en los planos una de sus mitades y siguiendo los criterios siguientes (ver Fig. 29):

–       Alzados: se representan generalmente con la proa a la derecha. Sobre ellos se trazan:

El perfil completo del barco (su intersección con el plano de crujía), en algunos casos, también se traza la quilla (caso de la Fig. 29, por ser un barco construido en madera).

Líneas de agua: todas se trazan paralelas entre sí y a la misma distancia unas de otras, aunque se pueden intercalar algunas, también paralelas a ellas, situadas a mitad de distancia. Las líneas de agua se numeran empezando por la 0, que es la que toca el barco en su(s) punto(s) más bajo(s) (la más gruesa de la Fig. 29) y se denominan con la abreviatura L.A., o sea que, habrá la L.A. 1, L.A. 2, L.A. 3, etc.  y si existiese otra comprendida entre la L.A. 1 y la L.A. 2, se llamaría L.A. 1½. Estas L.A. trazadas a mitad de distancia que las demás, se suelen colocar en aquellos sitios del barco donde existen fuertes cambios de forma. La cantidad de L.A. que deben trazarse, es una decisión del proyectista y depende mucho de los cambios de forma del barco; en los lugares de fuertes cambios de forma, conviene incrementar las L.A. Cuantas más L.A. se tracen, más perfecto será el barco que se obtenga de él, pero teniendo cuidado que un exceso no entorpezca el dibujo.

Cuadernas: siguen los mismos criterios de las L.A.

–       Plantas: se representa la mitad de babor del barco (cubiertas, líneas de borda y líneas de agua, entre otras), aunque hay quien representa el de estribor; representación que también incluye cuadernas y línea de crujía. Debido a ello, la distancia desde un punto de una línea de agua hasta la línea de crujía, se conoce con el nombre de semimanga en ese punto.

–       Perfiles, conocidos exclusivamente como caja de cuadernas: este conjunto de cuadernas, se traza a la derecha del alzado del barco, dibujándose a la derecha de la línea de crujía las cuadernas comprendidas entre la de mayor manga (generalmente conocida como maestra y representada en los planos con este símbolo ) y el extremo de proa y, a la izquierda de línea de crujía, las comprendidas entre la de mayor manga y el extremo de popa, de modo que solo la maestra se representa completa. La distancia desde un punto de una cuaderna hasta la línea de crujía, también se llama semimanga.

Fig. 29

Es obvio que el alzado, con dos líneas de agua y tres cuadernas, son completamente insuficientes para construir un modelo que se precie; si lo he hecho así es para no complicar, más de lo necesario, las explicaciones. Quiero recalcar de nuevo que, salvo las L.A de la planta., cuadernas del perfil y silueta del barco del alzado, todas las demás líneas rectas son paralelas, perpendiculares o ambas.

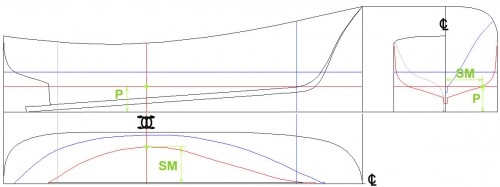
Todo punto del alzado, tiene necesariamente su correspondiente en la planta y en el perfil que, en conjunto, representan a un punto del barco. Ejemplo: en la Fig. 30 está localizado un punto verde en el alzado, planta y perfil, que es el cruce de la cuaderna roja con la L.A. del mismo color; para que este punto represente a su correspondiente del barco se tienen que dar las condiciones siguientes: las distancias P, deben ser exactamente iguales una a la otra y, las SM también, en caso contrario, el plano estará mal hecho y será ineludible su corrección. Esta filosofía es fundamental para un trazado correcto de cualquier plano de formas.

Fig. 30

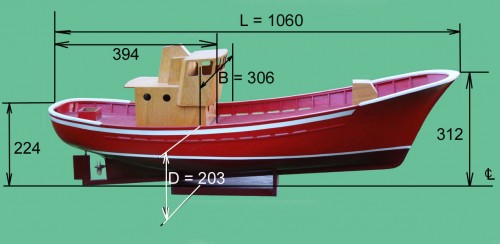
Afianzados estos conceptos fundamentales, explicaré ahora mi forma de trazar un plano de formas, aclarando previamente que, en esto como en otras muchas cosas, cada maestrillo tiene su librillo. Para esta explicación me valdré, de nuevo, de nuestro ya conocido pesquero del cantábrico, el de la Fig. 32. Este modelo tiene las siguientes características:

Eslora         (L)                                                                1060 mm

Manga        (B)                                                                 306 mm

Puntal extremo superior maestra (D)                  203 mm

Puntal en el extremo de popa                                  224 mm

Puntal en el extremo de proa                                   312 mm

Distancia de la maestra al extremo de popa       394 mm

Fig. 32

Definidos estos datos, trazo con ellos las líneas más gruesas (su grosor solo obedece a razones didácticas) que se ven en la Fig. 33, con lo que así quedan definidas las dimensiones principales del modelo. En concreto, el dimensionado es el que sigue:

Fig. 33

El resto de las líneas de la Fig. 33, están trazadas así:

Línea de borda 7-6-8: a criterio del proyectista, tanto en alzado como en planta (*).

Línea de popa, quilla y proa (alzado, naturalmente): a criterio del proyectista (*).

Línea azul: es la L.A. que coincide con la línea de flotación normal del modelo y su planta también se traza a criterio del proyectista (*).

Cuaderna maestra: a criterio del proyectista (*).

(*): Obviamente, no creo descubrir la pólvora, si afirmo que el proyectista debe inspirarse en otros planos (si los tiene a su alcance) o, en fotografías o, en ambos, para que sus trazados sean fieles al tipo de modelo que desea proyectar y, desde luego, su experiencia y “ojo clínico” deben jugar, también en esto, un papel fundamental.

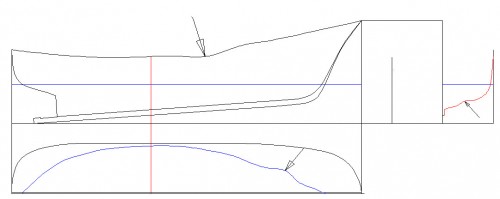
A quienes deseen “embarcarse” trazando un plano de formas, debo darles una pauta a seguir que creo fundamental para lograr el éxito en su aventura, ésta es: las líneas del casco de un barco, rara vez, presentan cambios bruscos de dirección, por lo que, si ello ocurre, debe hacer sospechar al proyectista que algo en la línea no es correcto. Para aclarar este concepto, fijémonos en la Fig. 34, he señalado con flechas unos tramos de línea que presentan un cambio anormal en su trazado (los he exagerado, pues frecuentemente son bastante imperceptibles), cuando esto ocurre debe investigarse y corregirse pues, de lo contrario, nos encontraremos con indeseadas irregularidades constructivas en el modelo, por ejemplo, oquedades o abultamientos.

Fig. 34

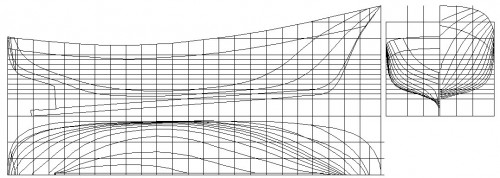
La Fig. 35 muestra el plano de formas completo del pesquero del cantábrico que me ha servido como guía en la redacción de muchas de estas líneas.

Fig. 35

Finalmente deseo decir que, lo que aquí explico, es lo básico que un proyectista naval debe conocer pues, tiene algunos intríngulis más, no obstante, quien domine lo que aquí he expuesto tendrá muchas posibilidades para descubrirlas por sí mismo.

Trazar un plano de formas sobre papel, como se hacía hace algunos años, es algo bastante tedioso y no exento de arduo trabajo, especialmente para quien no está habituado a ello; pero los ordenadores han venido a solucionar gran parte, sino todos, de estos problemas. Hoy es inimaginable realizar planos de formas sin recurrir al auxilio de un ordenador, razón por la que la totalidad de los modelos que he hecho, los he trazado gracias ellos. Deseo decir también, que el software de diseño naval actual es potentísimo y prácticamente ejecuta, casi solito, todos los conceptos y algunos más que aquí he explicado, aunque nunca los he utilizado, pero sí conozco por referencias. El software que utilizo es un CAD en el que introduzco, con toda la paciencia, los conceptos que aquí he tratado de explicar.

Dicho lo anterior, no es difícil deducir que con un ordenador se puede trazar con toda comodidad cualquier forma y tipo de línea; el problema se nos puede presentar cuando pretendamos trazarla sobre la madera que, tras su corte, formara parte del modelo. Para estos trazados, utilizo dos herramientas: las plantillas de curvas y los junquillos. Las primeras son conocidas por la mayoría de las personas que hayan tenido algún contacto con el dibujo lineal y los junquillos fueron muy utilizados en el pasado en las salas de proyectos navales, antes del advenimiento de los ordenadores. En la Fig. 36, muestro las plantillas de curvas y junquillo que utilizo en mis trazados sobre madera de piezas para modelos.

Fig. 36

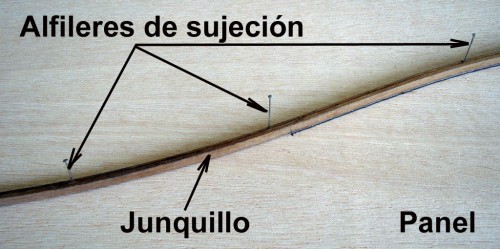
En la Fig. 37 se ve con más detalle la manera de utilizar el junquillo. Para empezar diré que el junquillo está hecho de con dos tablillas – de 5 x 1,5 mm de las utilizadas para el forrado de modelos – encoladas entre sí, a la que le he practicado unos agujeros en su dirección mayor que permiten el paso de  alfileres utilizados como método de sujeción del junquillo durante el trazado de la línea sobre la pieza de madera (panel, en el caso de esta Fig.)

Fig. 37

Antes de poner punto final a este ya largo escrito, deseo decir que el artilugio, del que tantas veces me he valido para muchas de las explicaciones, se llama académicamente triedro tri-rectángulo.

Corregiré cualquier error cometido en estas explicaciones, que alguien encuentre y me las comunique. Gracias.

Página principal:

http://ganandobarlovento.es/