Al desarrollo del tema aquí descrito le he dedicado una parte importante de mi tiempo libre; no obstante, soy consciente que a muy pocos interesará, pues, las tecnologías actuales resuelven lo descrito aquí en un «plis, plas» y, además, con mucha mayor comodidad, precisión y rapidez, bien es cierto que tienen el inconveniente de ser inasequibles económicamente para la mayoría de quienes nos gusta pasar el rato con temas navales, problema inexistente en la antigua pero lograda “tecnología” descrita aquí, que, además, está al alcance de cualquiera.
Con este relato manifiesto mi admiración y respeto a los pasados, presentes y futuros CARPINTEROS DE RIBERA ¡así, con mayúsculas!
Lo que sigue, es la descripción de una variante del método del «medio casco» utilizado en su día, entre otros, por los carpinteros de ribera para obtener las formas del casco de un barco. Definidas sus dimensiones principales se procede al trazado de los dos perfiles del casco que se desea construir; para esto último se traza la mitad del contorno exterior visto desde su parte superior – en general, es el contorno exterior de su cubierta intemperie -, y la vista del contorno lateral desde un costado, tal como se ven en 1.
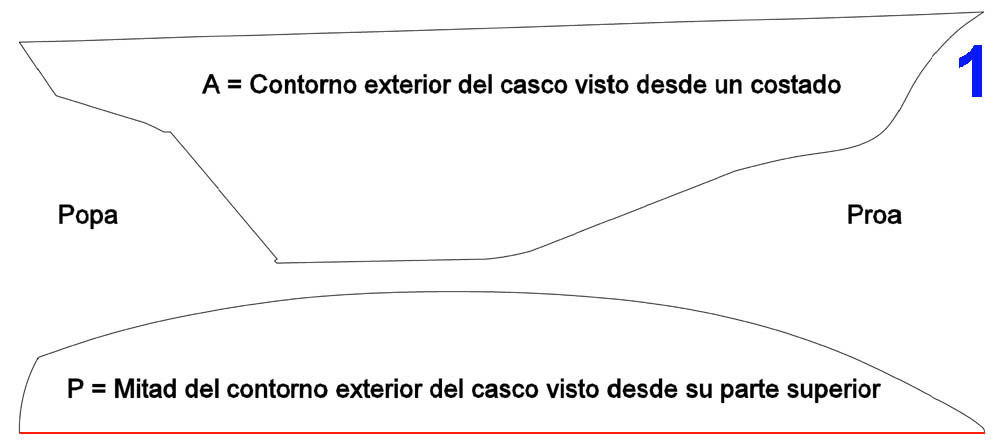
Puede que el perfil de costado mostrado le parezca raro a quienes no estén familiarizados con la parte sumergida de ciertas embarcaciones, por ello aclaro que corresponde a un velero de crucero de orza corrida que, probablemente, volveré a mencionar.
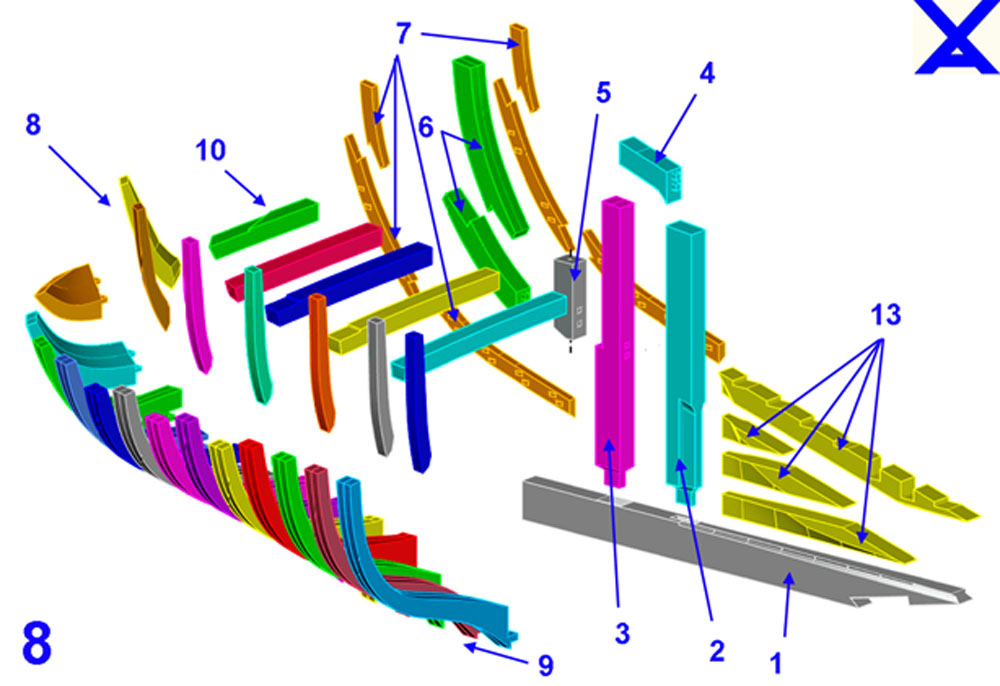
Como no podía ser de otra manera, el mencionado trazado se hacía a escala del barco real que representará – generalmente a 1/50 -, de modo que, con él ya es posible conocer las distancias entre cualquier par de puntos situados sobre la línea “A” o sobre la línea “P”, lo que da lugar a esta pregunta: ¿y qué pasa con los demás puntos? Para conocer el posicionamiento de todos los demás puntos situados sobre la superficie exterior del casco y, en consecuencia, la forma de este, recurriremos a la mencionada variante del método «medio casco» que consiste en confeccionar un semi modelo que se tallará a partir de un bloque de madera formado por, generalmente, láminas de 10 mm de espesor, aunque se puede elegir cualquier otro espesor (ver 2).

El tamaño de este bloque de madera deberá ser el suficiente como para que en su parte superior quepa el trazado “P” y en su lateral mayor el trazado “A”, antes mencionados, tal como muestra 3.
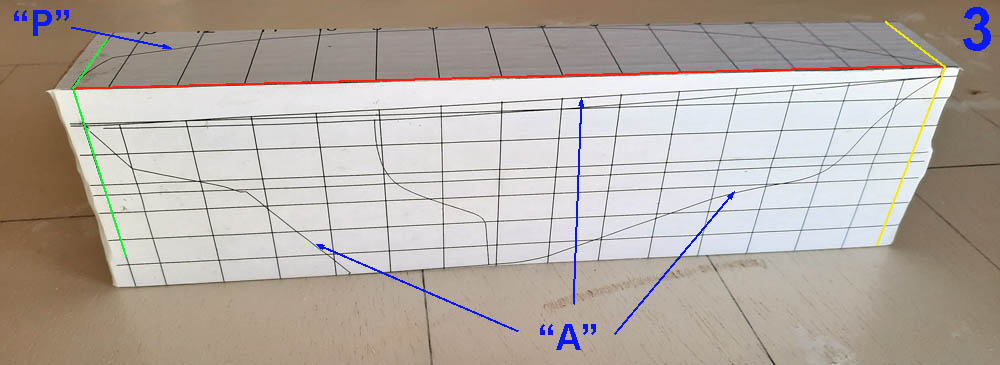
Los trazados “A” y “P” se pegarán sobre el bloque de madera, pero antes de hacerlo deberá estar lo más plano posible el lateral sobre el que se pegará el trazado “A”, además, esta operación de pegado deberá hacerse de tal manera que los extremos de ambos trazados se sitúen sobre los mismos planos perpendiculares a la superficie en la que se pone el trazado “A” que pasan por los extremos de proa y popa, señalados en 3 con las líneas verdes y amarillas; también la línea roja del trazado “P” debe coincidir exactamente con la arista que forman las dos superficies del taco en la que se peguen los trazados.
Hecho lo anterior, se recorta el taco de madera con una sierra siguiendo como líneas de corte los trazados “A” y “P”, como se aprecia en 4.

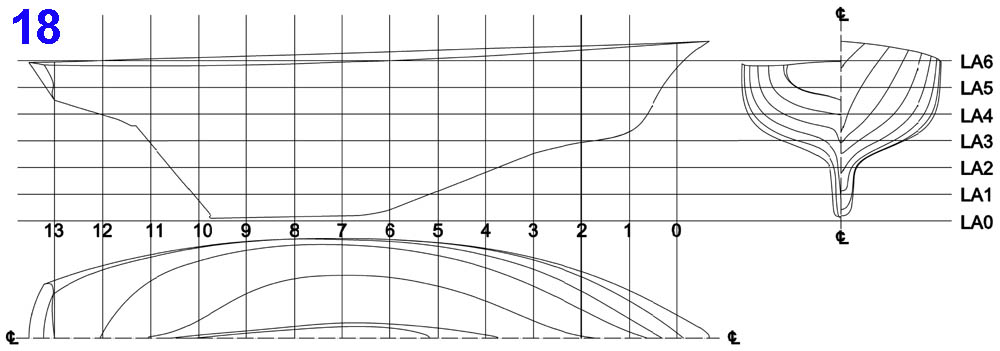
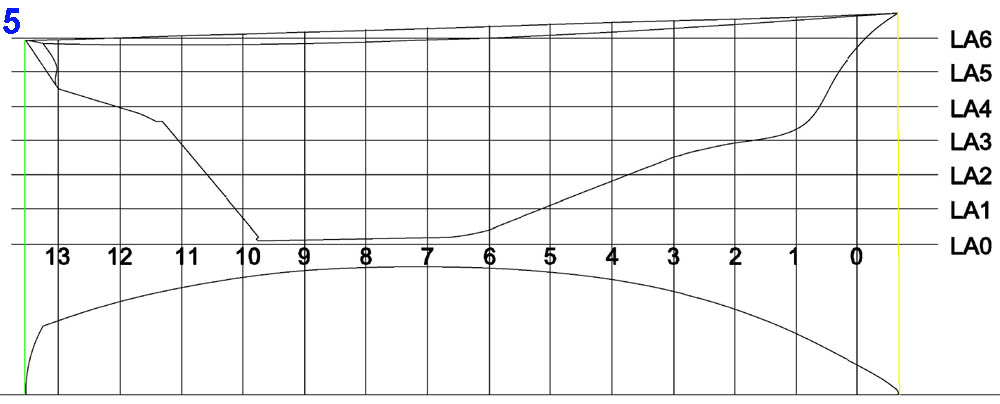
Llegados aquí conviene aclarar que, tras el dibujo de los contornos “A” y “P” – cuyos extremos deben situarse en las mismas líneas verticales (verde y amarilla) -, se trazaran sobre ellos líneas verticales equidistantes entre sí y otras horizontales igualmente equidistantes, tal como se ve en 5; a las primeras le llamaremos cuadernas que, convencionalmente, numeraremos de 0 a 13 (se puede elegir cualquier otra cantidad, pero no conviene que sean pocas) y a las segundas líneas de agua, a las que numeraremos LA0 a LA6. La distancia entre las LA será igual al espesor de las tablas utilizadas para confeccionar el ya mencionado bloque de madera. Todo esto explica la razón de las líneas existentes en los planitos pegados al bloque de madera.
La próxima etapa consiste en tallar la forma que queremos darle al casco y, sin entrar en ciertas consideraciones, creo que es un trabajo más próximo al de artista que al de técnico, de modo que, la imagen 6 muestra el tallado del casco que conseguí.

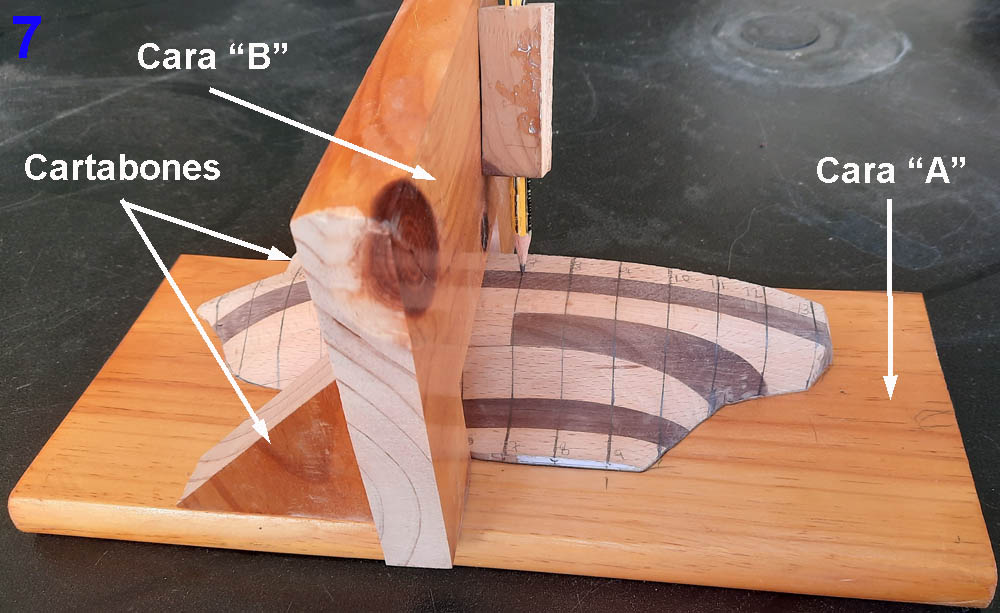
La escala de este semi modelo se ajustó únicamente al tamaño de las maderas que disponía en el momento de hacerlo, de modo que teniendo una longitud (eslora) de 258 mm, su escala con relación al mismo barco de longitud (eslora) 10 m (10.000 mm) es de aproximadamente 1/38, un tanto rara, pero es lo que podía hacer con la madera que tenía. En esta condición del semi modelo quedan perfectamente determinadas las líneas de agua, señaladas con flechas; ahora es necesario trazar las cuadernas sobre la superficie del casco y, para ello, hice un utillaje muy simple compuesto, básicamente, por dos tablas con sus caras perpendiculares entre sí, algo que se logra con los dos cartabones señalados en 7. La tabla vertical tiene una abertura que permite holgadamente el paso del semi modelo y no está unida a la cara “A”, lo que permite su libre desplazamiento por ella. Por la superficie de la cara “B” puede deslizarse un taquito de madera que sirve para alojar un lápiz, a la vez que ambos pueden moverse sujetos por la mano, pero manteniendo al taquito en contacto con esa cara mientras con el lápiz se trazan las cuadernas sobre la superficie del semi modelo.
Antes de trazar las cuadernas, se deben transferir sus extremos desde los planos pegados al semi modelo a la superficie labrada, tal como se ve en 8.

Hecho esto ya se pueden trazar las cuadernas colocando la cara “B” de manera tal que la punta del lápiz coincida con ambas marcas de cada cuaderna antes de trazar; hecho lo cual se hace el trazado, cuyo resultado es visible en 9.

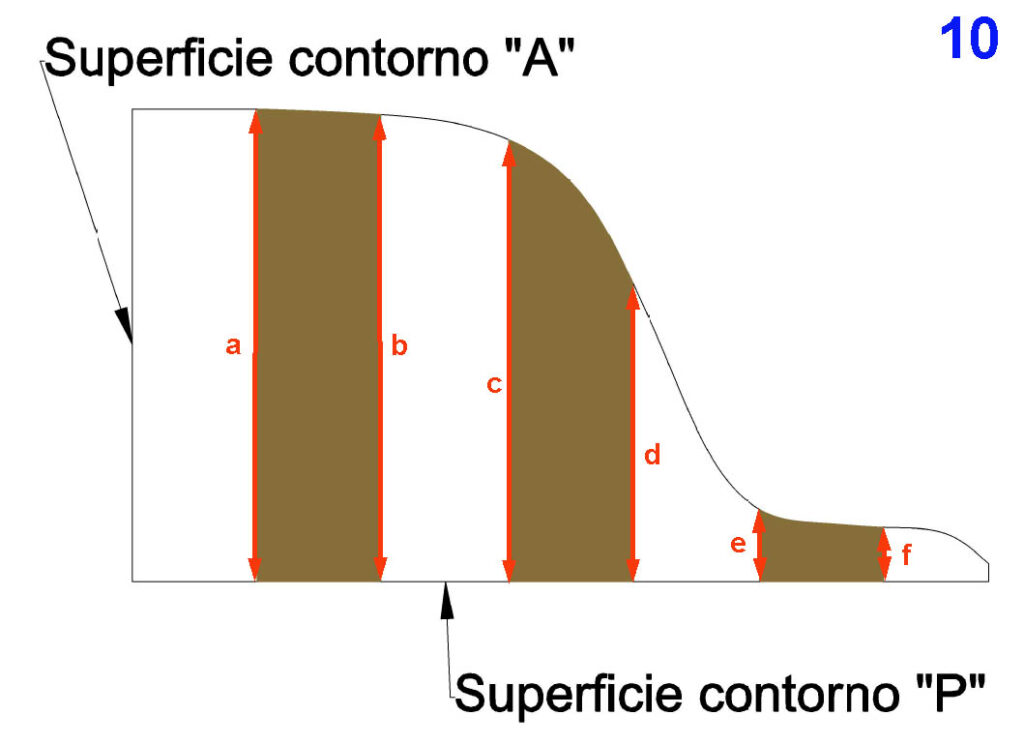
Ahora es posible trazar sobre el plano de la imagen 5 las formas reales de las líneas de agua y una tercera representación que incluya las formas de las cuadernas; para hacer esto es necesario conocer las distancias perpendiculares que van desde los puntos de cruce de las líneas de agua con las cuadernas hasta la cara del semi modelo donde está pegado el contorno “A”, o loque es lo mismo, hasta el plano donde se apoya esta cara del semi modelo. Aclararé esta idea algo más y, para ello, supongamos cortado el semi modelo siguiendo la línea de corte de la cuaderna 7 y, además, que este plano de corte sea perpendicular a la cara del semi modelo donde está pegado el contorno “A”, el contorno de esta sección tendría una forma bastante parecida a la mostrada en 10. Pues bien, las medidas a las que he hecho referencia son las señaladas en 10: ”a”, “b”, “c”. “d”, “e” y “f”
¿Y cómo se miden esas distancias en todas las cuadernas? Para eso preparé un dispositivo muy simple y similar al de hacer los trazados de las cuadernas sobre el semi modelo, tal como se aprecia en 11.
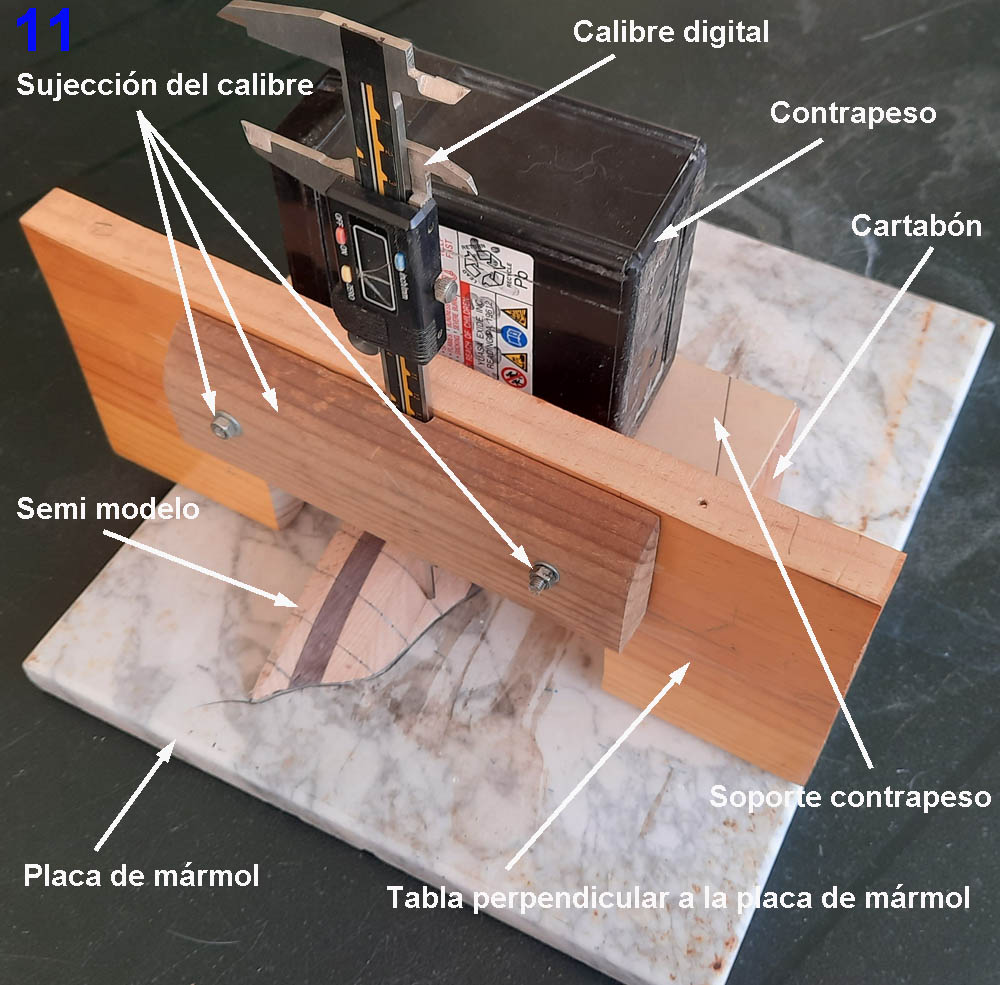
El “invento” está pensado para: tener las manos libres y así poder manejar el calibre; que se mueva libremente el conjunto soporte del calibre; que el puntero de este sea lo más perpendicular posible a la superficie de placa de mármol. El contrapeso solo sirve para mantener constantemente el ángulo de 90 º entre la tabla y el mármol, ángulo que generan dos cartabones (solo es visible uno) que además forman el soporte del contrapeso. Así pues, el método de medida de las mentadas distancias consiste en poner el extremo del puntero del calibre sobre la superficie del mármol poniendo el calibre a 0, y después colocarlo sobre las distintas intersecciones de cuadernas y líneas de agua para leer la lectura del calibre en esas posiciones que serán las medidas ”a”, “b”, “c”. “d”, “e” y “f” de las distintas cuadernas. La imagen 12 muestra la posición de medida de la distancia del punto que forman la LA3 con la cuaderna 2.

Las muchas medidas a tomar, aconseja registrarlas de manera ordenada; en este sentido, adopté el método siguiente:
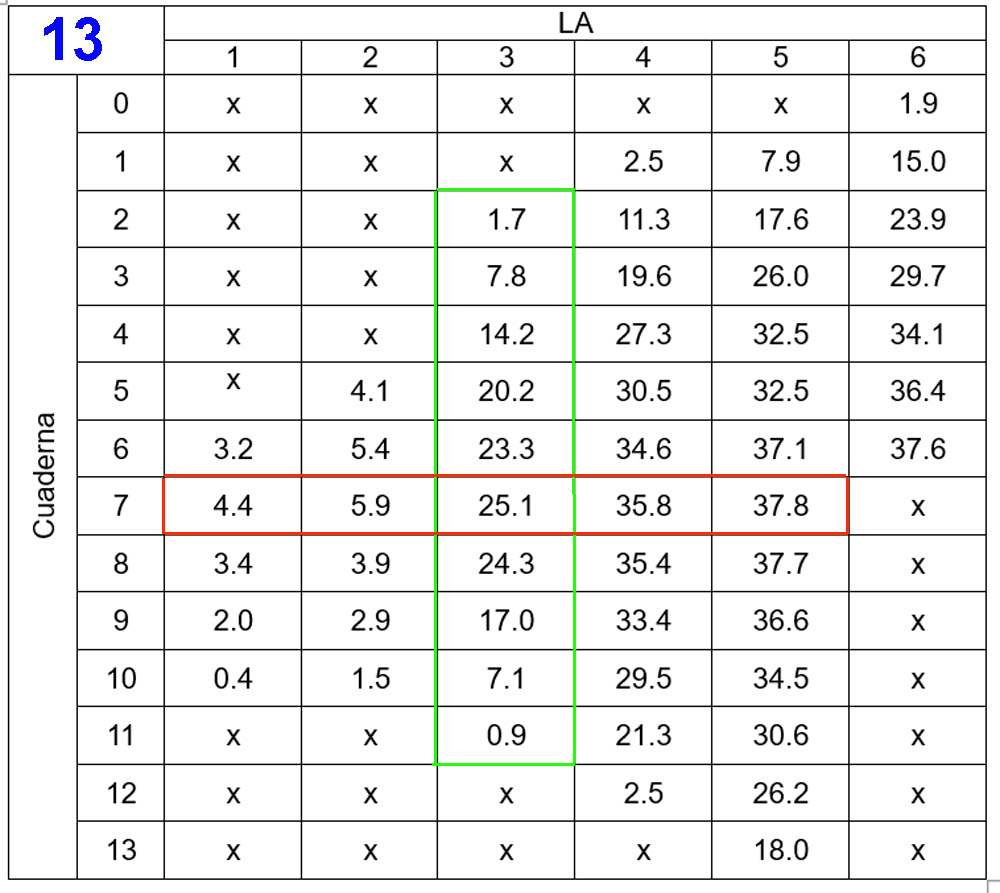
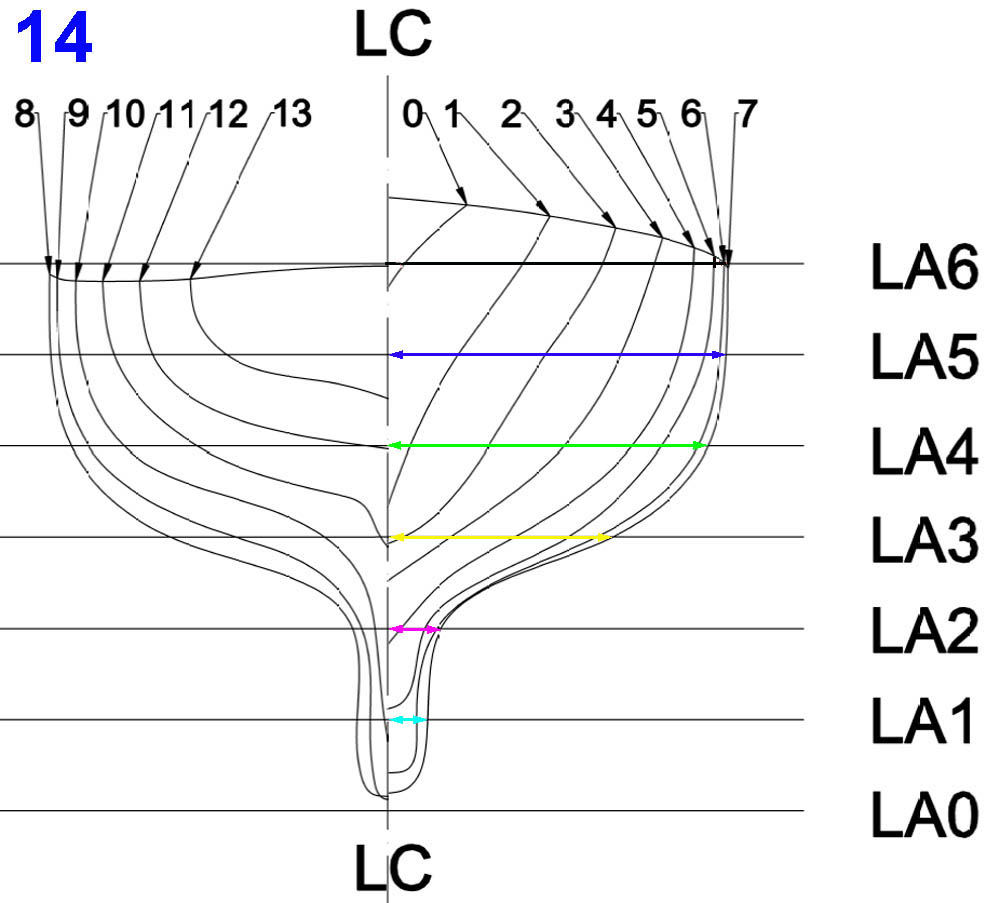
La representación gráfica de los datos de esa tabla se muestra en 14, o sea, LC-LC es una línea vertical, sin más, y las LA0 a LA6 también son líneas perpendiculares a ella cuyas distancias entre sí son iguales a los espesores de las maderas utilizadas para hacer el semi modelo. Ahora trazaremos sobre papel o en ordenador las líneas marcadas del 0 a 13 y, para ello, tomaré como ejemplo la señalada con 7 (todas sus compañeras se trazarán exactamente igual); iniciaremos el trazado situando los puntos de corte de la cuaderna con las distintas LA, para lo que tomaremos de la tabla anterior sus distancias a la línea LC-LC, o lo que es lo mismo, los valores enmarcados en rojo cuya correspondencia con la imagen 14 es:
distancia representada por la flecha:
cian: 4.4 mm;
fucsia: 5.9 mm;
amarilla: 25.1 mm;
verde: 35.8;
azul: 37.8 mm;
que, también corresponden a los valores “b”, “c”, “d”, “e” y “f” correspondientes a esta cuaderna, vistos en la imagen 10. A esta representación gráfica en la que las cuadernas se ven en su forma real (aunque a escala, claro), se conoce con el nombre de «caja de cuadernas», y la costumbre más extendida es representar las de la mitad de la eslora hacia popa, en la parte izquierda del dibujo, y el resto en su parte derecha. Una última observación, los pies de cuaderna (su parte más baja) se situarán sobre la línea LC-LC, y tomando como origen de distancias verticales la LA0, sus distancias a ella serán idénticas tanto en este plano como en el de la parte superior de la imagen 5. La parte alta de las cuadernas, «cabeza de cuaderna», se situará a la misma altura que el punto de corte de la línea de cubierta con la cuaderna, en el plano de la caja de cuadernas y el de la parte superior de la imagen 5; en ambos planos la distancia de este punto de cruce a la línea LC-LC, será idéntica. La línea que une todos estos puntos definidos así, es la línea de cubierta al costado (barcos de una sola cubierta).
Vista la representación real de las cuadernas, pasaremos ahora a representar gráficamente las LA (líneas de agua). Tomamos como ejemplo la LA3 (para las demás, se hace exactamente lo mismo) y, para ello (ver 15) se trazará la línea horizontal LC-LC y perpendiculares a ella trece líneas equidistantes y paralelas entre sí, tal como está representado en la imagen 5. Ahora, y sobre las distintas cuadernas, se llevarán las distancias encuadradas en verde de la tabla anterior, o sea:
Cuaderna distancia señalada en color valor en mm.
11 verde 0.9
10 rojo 7.1
9 azul 17.0
8 cian 24.3
7 amarillo 25.1
6 negro 23.3
5 gris 20.2
4 fucsia 14.2
3 naranja 7.8
2 verde oliva 1.7
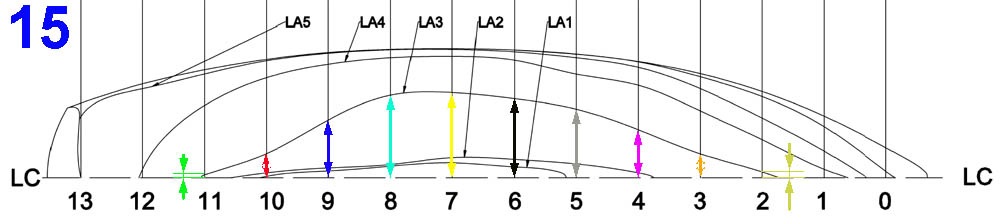
Insisto de que estas distancias deben ser idénticas a las de la caja de cuadernas para los mismos puntos de cruce de las distintas LA con las cuadernas.
Al conjunto de las representaciones gráficas descritas hasta aquí se conocen con el nombre de «plano de formas» y no «plano de líneas» como, a menudo, he visto escrito por ahí. Este es el nuestro:
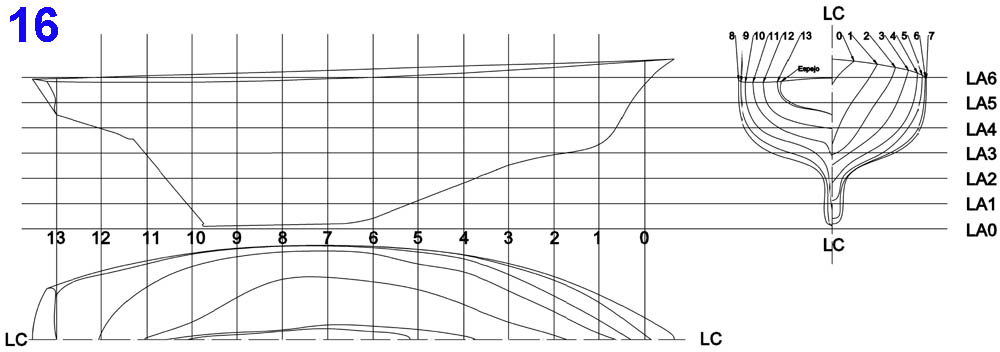
Casi todo lo que se hace tiene su nombre, y esto no es una excepción, de modo que al trazado superior izquierdo se le llama «alzado»; al superior derecho, «caja de cuadernas»; al inferior, «planta».
Ahora, si observamos el plano, es fácil percatarse de que muchas o todas las LA presentan “ondulaciones” impropias de un barco bien diseñado y construido, de modo que si se dejara tal como está y se construyera el barco, su casco tendría abultamientos y depresiones donde no debería haberlas. ¿Porqué ha ocurrido esto?: a consecuencia de una o varias de las siguientes razones:
- medidas tomadas incorrectamente con el calibre;
- imperfecto acabado superficial o forma del semi modelo;
- imprecisión en algún trazado hecho sobre el semi modelo;
- mal agarre del semi modelo al mármol (o base que se utilice), durante la toma de medidas;
- semi modelo demasiado pequeño o hecho a una escala demasiado reducida.
Lo dicho para las LA es perfectamente aplicable a la caja de cuadernas, aunque sus ondulaciones no se aprecien con tanta facilidad como en las LA.
El plano 17 es el mismo que el 16, excepto que en él están señalados con flechas, letras y círculos los puntos que, en un primer vistazo, provocan los abultamientos y depresiones antes mencionados que deben corregirse. En su día, esta operación era conocida con el nombre de «corrección de líneas»; y digo en su día, porque con las potentes tecnologías informáticas actuales (utilizadas fuera del ámbito doméstico), me parece muy improbable que no se haga de forma automatizada.
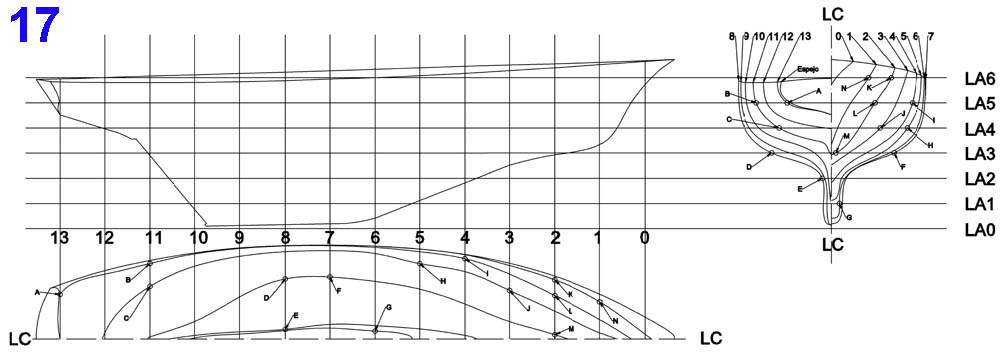
La corrección de líneas clásica consiste en separar o acercar los puntos erróneos (los mostrados) de las líneas de agua y de cuaderna con relación a las líneas LC-LC, de manera que, como ya antes se mencionó, sus distancias a ellas sean idénticas, tanto en la planta como en la caja de cuadernas. Si, ya se que puede ser un trabajo de paciencia y que requiere cierta experiencia, pero, siempre se ha hecho así hasta que la informática irrumpió con gran éxito en el diseño naval.
Efectuada la corrección de líneas, nuestro plano de formas quedó así: